Exercices Corrigés

Logique

Théorie de la preuve (du calcul des propositions)

Rappel: Un système de preuve pour le calcul propositionnel est constitué par un ensemble (éventuellement infini) de formules dites axiomes et par un ensemble fini de règles d’inférence qui établissent le façons admissibles de dériver des formules vraies à partir d’autres formules vraie.

Pour toutes formules $\phi,\psi,\chi$ on note $\vdash \phi$ si $\phi$ est démontrable uniquement à partir des axiomes en utilisant les règles d’inférence. On note $\phi,\chi\vdash\psi$ si $\psi$ est démontrable en ajoutant $\phi$ et $\chi$ aux axiomes et en utilisant les règles d’inférence.

Dans la suite nous allons prendre la liste (infinie) d’axiomes suivante:

1. $\phi\to(\psi\to\phi)$,
2. $(\neg\phi\to\neg\psi)\to(\psi\to\phi)$,
3. $(\phi \to (\psi\to\chi)) \to ((\phi\to\psi) \to (\phi\to\chi))$,
4. $\neg\neg\phi \to \phi$,
5. $\phi\to\phi$.
6. $(\psi\to\phi)\to(\neg\phi\to\neg\psi)$,

où $\phi,\psi,\chi$ sont des formules quelconques (par exemple $A$, ou $\neg A\to B$, etc.). La seule règle d’inférence de notre système est le modus ponens:

$$\dfrac{\phi\to\psi \qquad \phi}{\psi},$$

qui veut dire qu’à chaque fois qu’on a les formules $\phi\to\psi$ et $\phi$, on peut déduire $\psi$.

Les axiomes 1-3 sont dus à Łukasiewicz, les autres sont redondants (dans le sens qu’ils pourraient être dérivés des trois premiers), mais nous les ajoutons pour simplifier les preuves.

Question 1 Prouver que $A\vdash B\to A$.

Question 2 Prouver que $\neg B\vdash B\to A$.

Question 3 Prouver le raisonnement par contrapposée: $A\to B, \neg B \vdash \neg A$.

Question 4 On va montrer de d’une proposition fausse on peut déduire n’importe quoi. Nous choisissons $A\wedge\neg A$ comme proposition fausse.

1. Calculez sa table de vérité et vérifiez qu’elle est bien une antilogie.
2. Dans notre logique nous avons fait le choix d’utiliser seulement les symboles $\to$ et $\neg$. En utilisant les équivalences bien connues, transformez $A\wedge\neg A$ en une formule équivalente qui n’utilise que $\neg$ et $\to$. Vérifiez que les deux formules sont bien équivalentes à l’aide des tables de vérité.
3. Montrez que $\neg(A\to A)\vdash B$.

Question 5 Très difficile: montrez que l’axiome 6 peut être déduit des axiomes 1 et 3.

Solution

Dans les séquents qui suivent, on prend la convention de marquer une barre au dessus des hypothèses pour les distinguer des axiomes.

Question 1 Du premier axiome: $A\to(B\to A)$. En utilisant l’hypothèse $A$ et le modus ponens:

$$\dfrac{A\to(B\to A) \qquad \overline{A}}{B\to A}$$

Question 2 En appliquant les axiomes 1 et 2 et deux fois le modus ponens:

$$\dfrac{ (\neg A\to\neg B) \to (B \to A) \qquad \dfrac{ \neg B\to(\neg A\to\neg B) \qquad \overline{\neg B} }{\neg A\to\neg B} }{B\to A}$$

Question 3 En appliquant l’axiome 6 et deux fois le modus ponens:

$$\dfrac{ \dfrac{ (A\to B)\to(\neg B\to\neg A) \qquad \overline{A\to B} } {\neg B \to \neg A} \qquad \overline{\neg B} } {\neg A}$$

Question 4 On vérifie aisement que $A\wedge\neg A$ est une antilogie, ensuite on voit rapidement qu’une formule équivalente possible est:

$$\neg(A\to A)\equiv\neg(\neg A\vee A)\equiv\neg\neg A\wedge\neg A\equiv A\wedge\neg A.$$

Pour faire la preuve formelle, l’astuce consiste à instancier l’Axiome 1 en prenant $\phi=\neg(A\to A)$ et $\psi=\neg B$, cela donne

$$\neg(A\to A) \to (\neg B \to \neg(A\to A)).$$

Le reste suit aisement en invoquant les axiomes 2 et 5 et trois fois le modus ponens:

$$\dfrac{ \dfrac{ (\neg B\to\neg(A\to A)) \to ((A\to A)\to B) \qquad \dfrac{ \neg(A\to A) \to (\neg B \to \neg(A\to A)) \qquad \overline{\neg(A\to A)} } {\neg B \to \neg(A\to A)} } {(A\to A) \to B} \qquad A\to A }{B}$$

Question 5 On va prouver que $A\to A$ découle des axiomes 1 et 3. L’énoncé général suit immédiatement en remplaçant $A$ par une formule quelconque.

Il faut un bon coup d’intuition pour résoudre ce problème: l’astuce consiste à instancier l’axiome 3 de la façon suivante (en prenant $\phi=A,\psi=A\to A,\chi=A$)

$$(A\to((A\to A)\to A)) \to ((A\to(A\to A)) \to (A\to A))$$

Le reste de la preuve nécessite seulement de deux utilisations (presque évidentes) de l’axiome 1

$$\dfrac{ \dfrac{ (A\to((A\to A)\to A)) \to ((A\to(A\to A)) \to (A\to A)) \qquad A\to((A\to A)\to A) }{(A\to(A\to A)) \to (A\to A)} \qquad A\to(A\to A) }{A\to A}$$

Partiel 2010

Métro

Considérons le plan de métro de Paris. Soit $M$ l’ensemble des stations de métro.

1. Soit $\mathcal{R}$ la relation sur $M\times M$ suivante: Soit $x$ et $y$ deux stations de métro, on a $x\mathcal{R}y$ si et seulement si $x$ et $y$ sont sur la même ligne. Quelles sont les propriétés de $\mathcal{R}$?
2. Sot $\mathcal{F}$ la relation sur $M\times M$ suivante: Soit $x$ et $y$ deux stations de métro, on a $x\mathcal{F}y$ si et seulement si un passager peut aller de $x$ vers $y$ en métro. Quelles sont les propriétés de $\mathcal{F}$?

Solution

1. La relation est réflexive et symétrique. En effet $x$ est sur la même ligne que lui même, si $x$ est sur la même ligne que $y$ alors $y$ est sur la même ligne que $x$. La relation n’est pas transitive: en effet Cité et Raspail sont sur la ligne 4, Raspail et Picpus sont sur la ligne 6, mais Cité et Picpus ne sont pas sur la même ligne.
2. Il s’agit d’une équivalence. En effet la réflexivité et la transitivité sont claires. La symétrie est moins claire (pensez à la ligne 10 qui fait une boucle vers la fin), mais on constate tout de même que si on ne peut pas prendre le métro en sens inverse, on peut au pire faire une boucle pour revenir à la station de départ.

Monnaie

Nous considérons des pièces de monnaie de 1, 2, 5 centimes. Notons $N(x)$ le nombre minimum de pièces pour obtenir $x$ centimes.

1. Quelle est la valeur de $N(0), N(1), N(2), N(3), N(4), N(5)$?
2. Trouver la relation sous forme mathématique de $N(x)$ en fonction des valeurs $N(w)$ avec $w < x$.
3. Prouver cette formule par induction/récurrence sur $x$.

Solution

1. $N(0) = 0$, $N(1) = N(2) = N(5) = 1$, $N(3)=N(4)=2$.
2. J’affirme que $N(x) = \min(N(x-1), N(x-2), N(x-5)) + 1$ pour tout $x > 5$.
3. Soient $n_1=N(x-1), n_2=N(x-2), n_5=N(x-5)$. Très clairement en ajoutant respectivement 1, 2, ou 5 centimes on obtient une façon de composer $x$ centimes en utilisant $n_1+1$, $n_2+1$ et $n_5+1$ pièces respectivement. Donc $N(x) \le \min(n_1,n_2,n_5) + 1$. Supposons maintenant que $N(x) = n < \min(n_1,n_2,n_5)+1$. Nécessairement $n>0$, puisque $x>0$. Supposons, sans perte de généralité, que dans les $n$ pièces pour obtenir $x$ il y en ait au moins une de $1$ centime, alors en ôtant cette pièce on a une façon d’obtenir $x-1$ centimes en utilisant seulement $n-1 < n_1$ pièces, ce qui contredit l’hypothèse que $n_1=N(x-1)$. On conclut que $N(x)=\min(n_1,n_2,n_5)+1$.

Récurrence

Considérons la suite $Z$ telle que $Z(1)=1$ et $Z(n)=Z(\lceil\frac{n}{2}\rceil) + Z(\lfloor\frac{n}{2}\rfloor) + 1$. Montrer que

$$\forall n\ge2, Z(n)\le cn-b$$

en fixant les variables $c$ et $b$.

Solution

On commence par calculer quelques termes de la récurrence.

$$Z(1)=1, Z(2) = Z(1)+Z(1)+1 = 3, Z(3) = Z(2)+Z(1)+1 = 5, Z(4)=7, Z(5) = 9,\ldots$$

On dirait que la valeur de $Z(n)$ grandit à peu près comme le double de $n$. Si on regarde bien, on s’aperçoit que $Z(n)=2n-1$. Une possibilité consiste à faire le pari que cette égalité est bonne et à essayer de la prouver par récurrence.

Nous allons procéder d’une façon différente en faisant une induction à reculons. Nous allons laisser les valeurs de $c$ et $b$ indeterminées et nous allons quand même faire la preuve, en commençant par le cas inductif. Ceci va nous permettre de trouver des contraintes sur $c$ et sur $b$. Ensuite nous allons travailler le cas de base pour résoudre les indeterminées qui restent.

Supposons $Z(n)\le cn-b$, alors

$$Z(2n) = 2Z(n)+1 \le 2cn-2b+1 = c(2n)-b + (1-b)$$

Donc pour que $Z(2n)\le c(2n)-b$ on a nécessairement $b\le1$. Choisissons la valeur limite $b=1$ et recommençons la preuve. Supposons $Z(n)=cn-1$, alors

$$Z(2n) = 2Z(n)+1 \le 2cn-2+1 = c(2n)-1,$$ $$Z(2n+1) = Z(n)+Z(n+1)+1 \le c(n+1) -1 + cn - 1 + 1 = c(2n+1) - 1.$$

Tout va bien, donc, il ne nous reste qu’à trouver un $c$ qui fait marcher le cas de base. On a

$$3 = Z(2) \le 2c - 1$$

d’où on déduit $c\ge 2$, donc on peut prendre $c=2$. On vérifie que l’inégalité est en fait une égalité.

Fonctions

Soit $X,Y$ deux ensembles finis. Soit $f:X\to Y$ une application. Montrer que

1. Si $f$ est surjective et si $B$ est un sous ensemble de $Y$, alors $f(f^{-1}(B)) = B.$
2. Si $f$ est injective et si $A$ est un sous ensemble de $X$, alors $f^{-1}(f(A)) = A.$

Supposons que $X,Y$ sont deux ensembles finis de même cardinalité. Montrer que

1. Si $f$ est injective alors $f$ est surjective.
2. Si $f$ est surjective alors $f$ est injective.

Solution

Pour l’instant nous n’avons pas besoin de l’hypothèse que $X$ et $Y$ sont finis.

1. Soit $b\in B$. Puisque $f$ est surjective il existe $a\in X$ tel que $f(a)=b$. Mais alors $a\in f^{-1}(B)$ et donc $b\in f(f^{-1}(B)$. Inversement soit $b\in f(f^{-1}(B))$, alors par définition il existe $a\in f^{-1}(B)$ tel que $f(a)=b$. Mais alors par définition de $f^{-1}(B)$ il existe $b'\in B$ tel que $f(a)=b'$, donc $b=b'$ puisque $f$ ne peut prendre deux valeurs en $a$. On conclut que $b\in B$.
2. Soit $a\in A$ et soit $b=f(a)$, alors $a\in f^{-1}(b)$, du coup $a\in f^{-1}(f(A))$. Soit $a\in f^{-1}(f(A))$, par définition il existe $b\in f(A)$ tel que $f(a)=b$. Mais $b\in f(A)$ implique qu’il existe $a'\in A$ tel que $f(a')=b$. Comme $f$ est injective $a=a'$ et $a\in A$.

Maintenant il devient important d’utiliser la finitude de $X$ et $Y$.

1. Soit $n$ la cardinalité de $X$. Puisque $f$ est injective, à chaque élément de $X$ correspond un unique élément de $Y$. Donc l’image de $f$ a cardinalité $n$ et correspond à $Y$ tout entier.
2. Supposons que $f$ ne soit pas injective, alors il existe $x,x'\in X$ tels que $f(x)=f(x')$. On considère l’ensemble $A=X\backslash\{x,x'\}$ de cardinalité $n-2$, son image par $f$ a cardinalité au plus $n-2$. Donc l’image de $X$ tout entier par $f$ a cardinalité au plus $n-1$ ($n-2$ de $A$, plus $1$ de $\{x,x'\}$), ce qui contredit la surjectivité.

Encore des fonctions

Existe-t-il

1. Une application non-surjective et non-injective.
2. Une application non-surjective et injective.
3. Une application surjective et non-injective.

Solution

Oui, elles existent toutes. Une façon simple d’en montrer des exemples c’est de dessiner des diagrammes de Venn finis (des ensembles avec un ou deux éléments suffisent). Nous allons donner des exemples un peu plus intéressants de fonctions de $\mathbb{R}$ dans lui même:

1. Le sinus et le cosinus.
2. L’arc tangente.
3. La fonction $x^3-x$.

Équivalence binaire

Soit $k$ un entier. $S_k$ l’ensemble des entiers compris entre $0$ et $2^k-1$. Soit $\mathcal{R}$ une relation d’équivalence $S_k\times S_k$ définie de la façon suivante: on a $x\mathcal{R}y$ si et seulement si le nombre de bits de la représentation binaire de $x$ est égal au nombre de bits de la représentation binaire de $y$.

• Montrer que $\mathcal{R}$ est une relation d’équivalence.

Solution

$\mathcal{R}$ est une relation d’équivalence par hypothèse: c’est écrit dans la définition. Blagues à part, vérifions que c’est bien le cas:

• Elle est réflexive: $x$ a le même nombre de bits que lui même.
• Elle est symétrique: si $x$ a le même nombre de bits que $y$, alors $y$ a le même nombre de bits que $x$.
• Elle est transitive: si $x$ a le même nombre de bits que $y$, et $y$ a le même nombre de bits que $z$, alors $x$ a le même nombre de bits que $z$.

Partiel Novembre 2011

Changements de base

Effectuer les changements de base suivants

1. $(10011)_2$ en décimal, $(64*19+3)_{10}$ en binaire.
2. $(54321)_{16}$ en binaire, puis en base 8.
3. $(1101 1101 1101,1101)_2$ en héxadécimal

Solution

1. $(10011)_2 = (19)_10$, ce qui se vérifie par un simple calcul. $(64*19+3)_10 = 2^6*(10011)_2 + (11)_2$; multiplier par une puissance de $2$ revient à ajouter des $0$ à droite, donc $2^6*(10011)_2=(10011000000)_2$; maintenant il est aisé de faire la somme directement en base $2$, le résultat est $(10011000011)_2$.
2. Un chiffre en base $16$ correspond à $4$ chiffres en base $2$. On convertit chaque chiffre et on a $(1)_16=(0001)_2, (2)_16=(0010)_2, (3)_16=(0011)_2, (4)_16=(0100)_2, (5)_16 = (0101)_2$. Donc $(54321)_16=(101.0100.0011.0010.0001)_2$ (j’ajoute les points pour aider la lisibilité). Maintenant on regroupe les bits par paquets de 3 et on convertit vers la base $8$. On a $(001)_2=(1)_8, (100)_2=(4)_8, (010)_2=(2)_8$, donc $(1.010.100.001.100.100.001)_2=(1241441)_8$.
3. $(1101)_2=(13)_10=(D)_16$, donc $(1101.1101.1101,1101)_2=(DDD,D)_16$.

Induction, pair-impair

Prouver par induction que pour tout $x$ et tout entier $n$

$$(-x)^n = \begin{cases} x^n &\text{si}\quad n\quad\text{est pair,}\\ -x^n &\text{sinon.} \end{cases}$$

Solution

Il y a plusieurs façons de poser l’induction. Nous allons choisir celle qui utilise le moins de cas de base possibles.

Cas de base: $(-x)^0 = 1 = x^0$, donc la thèse est bien vérifiée car $0$ est pair.

Cas inductif: Supposons la thèse vraie pour un certain $n\in\mathbb{N}$ pair, alors $n+1$ est impair et $(-x)^{n+1} = (-x)^n (-x) = x^n(-x) = -x^{n+1}$, où la deuxième égalité découle de l’induction.

De la même façon, supposons la thèse vraie pour un certain $n\in\mathbb{N}$ impair, alors $n+1$ est pair et $(-x)^{n+1}=(-x)^n(-x)=-x^n(-x)=x^{n+1}$.

Par induction, nous concluons que la thèse est vraie pour tout $n\in\mathbb{N}$.

Inductions

Prouver par induction les (in)égalités suivantes

1. $\sum_{i=0}^n i(i-1) = \frac{n(n^2-1)}{3}$.
2. $3^n\le(2n)!$ pour tout $n\ge2$.
3. $2^n n\le3^n$ pour tout $n\ge0$.

Solution du point 1

Vérifions la thèse pour $n=0$.

$$\sum_{i=0}^0 i(i-1) = 0(-1) = 0 = \frac{0(-1)}{3}.$$

Maintenant supposons la thèse vraie pour un certain $n$, alors

$\sum_{i=0}^{n+1} i(i-1) = n(n+1) + \sum_{i=0}^n i(i-1) =$ $n\left(\frac{n^2-1}{3} + (n+1)\right) = n\frac{n^2+3n+2}{3} = \frac{n(n+1)(n+2)}{3} =$ $\frac{(n+1)(n^2+2n)}{3} = \frac{(n+1)((n+1)^2-1)}{3}.$

On conclut par induction.

Solution du point 2

Vérifions la thèse pour $n=2$.

$$3^2 = 9 \le 24 = 4!.$$

Maintenant supposons la thèse vraie pour un certain $n$, alors

$$3^{n+1} = 3\cdot 3^n \le 3 \cdot (2n)! \le (2n)!(2n+1)(2n+2) = (2n+2)!,$$

où l’on fait bien attention à vérifier que $(2n+1)(2n+2)\ge 3$ pour tout $n\ge 2$.

Solution du point 3

Il y a plusieurs solutions raisonnables pour cet exercice, nous allons en choisir une qui utilise une double induction. Pour cela nous allons avoir besoin de montrer quelques cas de base en plus (la raison sera claire plus loin).

Pour $n=0,1,2$ on a

• $2^0 \cdot 0 = 0 \le 1 = 3^0$,
• $2^1 \cdot 1 = 2 \le 3 = 3^1$,
• $2^2 \cdot 2 = 8 \le 9 = 3^2$.

Maintenant supposons l’hypothèse vraie pour un $n\ge 2$, alors

$$2^{n+1}(n+1) = 2^{n+1}n+2^{n+1} = 2\cdot 2^n n + 2^{n+1} \le 2\cdot 3^n + 2^{n+1},$$

où l’inégalité découle de l’hypothèse d’induction. Si l’on arrive à montrer que $2^{n+1}\le 3^n$, alors on a fini car on déduit

$$2^{n+1}(n+1) \le 2\cdot 3^n + 2^{n+1} \le 3\cdot 3^n = 3^{n+1}.$$

Pour démontrer $2^{n+1}\le 3^n$, on s’y prend à nouveau par induction. Ceci est faux pour $0$ et $1$ (voici pourquoi on a démontré quelques cas de base en plus), mais à partir de $n=2$ on a

$$2^3 = 8 \le 9 = 3^2.$$

Maintenant on suppose $2^{n+1}\le 3^n$ vrai pour un certain $n\ge 2$, alors

$$2^{n+2} = 2\cdot 2^{n+1} \le 2\cdot 3^n \le 3\cdot 3^n = 3^{n+1}.$$

On conclut par induction.

Ensemble des parties et bits

On fixe un $n\in\mathbb{N}$ quelconque. Soit $H_n=\{0,1\}^n$ l’ensemble des chaînes de bits de longueur $n$ (par exemple $0101$ est un élément de $H_4$).

• Combien d’éléments contient $H_n$?

Pour chaque $0 < i\le n$ on définit la fonction $\delta_i:H_n\to\{0,1\}$ comme suit

$$\delta_i(x) = \begin{cases} 0 &\text{si le $i$-ème bit de $x$ en partant de la droite est $0$,}\\ 1 &\text{sinon}. \end{cases}$$

Par exemple, $\delta_1(1010) = 0$.

• On fixe $n=4$. Quelle est la cardinalité de $\delta_i^{-1}(0)$, pour $i=1,\ldots,4$?
• Pour quelles valeurs de $n$ et $i$ les fonctions $\delta_i$ sont-elles injectives? surjectives? bijectives?

Soit $\mathcal{R}$ la relation sur $H_n$ définie par $x\mathcal{R}y$ si et seulement si pour tout $0 < i\le n$, $\delta_i(y)\ge\delta_i(x)$.

• $\mathcal{R}$ est-elle un ordre? Est-elle totale? En donner les preuves, ou montrer des contre-exemples.
• Dessiner le diagramme de Hasse de $\mathcal{R}$ pour $n=3$.
• Soit $A=\{1,2,3,4\}$. Définir une bijection entre $H_4$ et $\mathcal{P}(A)$.

Solution

$H_n$ est l’ensemble des chaînes composées d’exactement $n$ bits. Par exemple on a

• $|H_0| = |\{\varepsilon\}| = 1$ (où $\varepsilon$ represente la chaîne vide),  
• $|H_1| = |\{0,1\}| = 2$,  
• $|H_2| = |\{00,01,10,11\}| = 4$,  
• $|H_1| = |\{000,001,010,011,100,101,110,111\}| = 8$.  

Il est alors facile de voir que $|H_n|=2^n$, en effet on a deux choix pour chaque bit et il faut faire au total $n$ choix.

L’argument ci-dessus suffit en général à convaincre un mathématicien, mais si on voulait être formels jusqu’à la moelle on pourrait montrer $|H_n|=2^n$ par induction: les cas de base sont déjà donnés en haut, pour le cas inductif on observe que le premier bit peut être fixé à soit à $0$ soit à $1$, et que les autres bits forment une chaîne de $n-1$ bits, alors $|H_n| = 2|H_{n-1}| = 2\cdot 2^{n-1} = 2^n$, où la deuxième égalité découle de l’hypothèse d’induction.

Maintenant la fonction $\delta_i$ associe à une chaîne quelconque de $H_n$ la valeur de son $i$-ième bit, donc l’image inverse $\delta_i^{-1}(0)$ est l’ensemble de toutes les chaînes de $H_n$ ayant le $i$-ème bit à $0$. Fixons $n=4$ et étudions, par exemple, $\delta_1^{-1}(0)$, on a

$$|\delta_1^{-1}(0)| = |\{0000, 0010, 0100, 0110, 1000, 1010, 1100, 1110\}| = 8.$$

Il s’agit, en effet, de l’ensemble des chaînes de longueur $3$ auxquelles on a ajouté tout à droite un bit égal à $0$. Il est maintenant clair que pour $i=1,2,3,4$ on a toujours la même structure: toutes les chaînes de $H_3$ auxquelles on a ajouté un $0$ en position $1,2,3$ ou $4$. Donc $|\delta_i^{-1}(0)|=8$ pour $i=1,2,3,4$.

Pour $n=0$ il n’existe aucune fonction $\delta_i$ (car par définition $0 < i\le n$). Pour $n=1$, la fonction $\delta_1:\{0,1\}\to\{0,1\}$ est la fonction définie par $0\mapsto 0$ et $1\mapsto 1$, donc elle est injective et surjective (et donc, par définition, bijective). Pour $n>1$ les fonctions $\delta_i$ ne sont plus injectives, par exemple $\delta_1(00)=\delta_1(10)=0$, par contre elles sont toutes surjectives, en effet pour chaque position $i$ il y aura toujours une chaîne qui a un $0$ ou un $1$ en cette position.

La relation $x\mathcal{R}y$ est un ordre partiel (non total). En effet, elle est:

• Réflexive: pour tout $x$ et tout $0 < i\le n$ on a $\delta_i(x)=\delta_i(x)$.
• Transitive: soient $x,y,z\in H_n$. Pour un $i$ quelconque, si $\delta_i(y)\ge\delta_i(x)$ et si $\delta_i(z)\ge\delta_i(x)$ alors $\delta_i(z)\ge\delta_i(x)$. Donc $x\mathcal{R}y$ et $y\mathcal{R}z$ impliquent $x\mathcal{R}z$.
• Anti-symétrique: supposons $x\mathcal{R}y$ et $y\mathcal{R}x$, alors pour tout $0 < i\le n$ on a $\delta_i(y)\ge\delta_i(x)$ et $\delta_i(x)=\delta_i(y)$, d’où on déduit $\delta_i(x)=\delta_i(y)$. Mais deux chaînes de $n$ bits qui coïncident en tout bit sont identiques, donc $x=y$.
• Non totale: en effet on a ni $01\,\mathcal{R}\,10$, ni $10\,\mathcal{R}\,01$.

En conclusion, voici le diagramme de Hasse de $\mathcal{R}$:

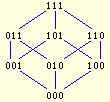
En fait, tout l’exercice tourne autour d’un isomorphisme bien connu et souvent utilisé en informatique entre l’ensemble $H_n$ et l’ensemble des parties $\mathcal{P}(A)$ d’un ensemble $A$ quelconque à $n$ élèments. On rappelle que l’ensemble $\mathcal{P}(A)$ est l’ensemble de tous les sous-ensembles de $A$. L’idée consiste à représenter un sous-ensemble $B\subset A$ par une chaîne qui contient un $1$ pour chaque élément de $A$ présent dans $B$ et un $0$ pour chaque élément de $A$ qui n’est pas dans $B$; ceci nécessite de choisir un ordre arbitraire sur les éléments de $A$ (ce qui est aisé puisque $A$ est fini).

Par exemple, pour $n=4$, soit $A=\{1,2,3,4\}$. On écrit les éléments de $A$ en ordre décroissant (il s’agit juste d’une convention, on aurait aussi bien pu choisir l’ordre croissant ou tout autre ordre non-standard) comme ci-dessous

$$\begin{array}{r c c c c l} A = \{ & 4, & 3, & 2, & 1 & \}\\ & 1 & 0 & 0 & 1 \end{array}$$

alors la chaîne $1001$ représente le sous-ensemble $B=\{1,4\}\subset A$, la chaîne $0000$ représente l’ensemble vide, la chaîne $1111$ représente $A$ tout entier, et ainsi de suite.

Grace à cet isomorphisme, qu’on va noter $\phi:H_4\to A$, on peut reinterpréter $\delta_i$ et $\mathcal{R}$ en termes d’opérations ensemblistes. En effet,

• $\delta_i$ correspond à l’appartenance: $\delta_1(x) = 1 \Leftrightarrow 1\in\phi(x)$, $\delta_2(x)=1\Leftrightarrow 2\in\phi(x)$ et ainsi de suite.
• $\mathcal{R}$ correspond à l’inclusion: $x\mathcal{R}y\Leftrightarrow\phi(x)\subset\phi(y)$.

Pour terminer, on remarque tout de même que, comme $\mathcal{P}(A)$ et $H_4$ ont la même cardinalité (à savoir $16$ éléments), il aurait été aussi aisé de donner une bijection quelconque en donnant la liste des couples élément-image, sans besoin de comprendre la théorie qu’il y avait derrière.

Encore des bits

Soit $H^\ast=\{0,1\}^\ast=\bigcup_{n>0}H_n$ l’ensemble de toutes les chaînes de bits de longueur arbitraire.

• Quelle est la cardinalité de $H$? Justifiez votre réponse en exhibant une bijection avec $\mathbb{N}$.

Pour tout $i>0$, on définit la fonction $\delta_i:H\to\{0,1\}$ qui associe à un mot $x\in H$ la valeur de son $i$-ème bit en partant de la droite, ou $0$ si $x$ a moins de $i$ bits. Par exemple $\delta_1(10)=\delta_5(10)=0$.

On définit enfin la fonction $w:H\to\mathbb{N}$ qui associe à un mot $x\in H$ son \textit{poids de Hamming}, c’est à dire son nombre de $1$. Par exemple $w(01101)=3$.

• La fonction $w$ est elle injective? surjective? bijective?
• Énumérer les éléments de $w^{-1}(3)\cap w^{-1}(5)$.

Les relations suivantes sont-elles réflexives? symétriques? transitives?

• $x\mathcal{S}y$ si et seulement si $\delta_1(x)=\delta_3(y)$;
• $x\mathcal{U}y$ si et seulement s’il existe un $i>0$ tel que $\delta_i(x)=\delta_2(y)$.
• $x\mathcal{T}y$ si et seulement si $w(x)=w(y)$;

Justifiez vos réponses.

On note $\overline{x}$ la classe d’équivalence de $x\in H$ pour la relation $\mathcal{T}$ donnée au point précédent. Soit $H_n\subset H$ l’ensemble des chaînes de longueur $n$.

• Énumérer les éléments de $\overline{0110}\cap H_n$ pour $n=2,3,4$.
• On note $C(n)$ la cardinalité de $\overline{0110}\cap H_n$. Exprimez $C(n)$ en fonction de $C(n-1)$.
• Prouvez par induction que $C(n) = n(n-1)/2$.

Solution

$H$ est évidemment un ensemble infini. Comme la question le suggère, il est dénombrable car il est en bijection avec les nombres naturels. On pourrait être tenté de définir la bijection $H\to\mathbb{N}$ tout simplement en lisant les éléments de $H$ comme des nombres en base $2$, cependant ce choix n’est pas adapté car $001$ et $1$ sont deux éléments distingués de $H$, mais il représentent le même nombre en base $2$.

Une astuce possible consiste à rajouter un $1$ à gauche des éléments de $H_n$ et ensuite à lire le résultat comme l’écriture en base $2$ d’un nombre. Par exemple:

• $\varepsilon \mapsto (1)_2 = 1$,
• $0 \mapsto (10)_2 = 2$,
• $1001 \mapsto (11001)_2 = 25$,
• $0011 \mapsto (10011)_2 = 19$.

Or, il est facile de se convaincre que cette fonction est bien injective, mais il est aussi évident qu’elle n’est pas surjective car $0\in\mathbb{N}$ n’a pas d’antécédent. Heureusement il est facile de résoudre ce problème: il suffit de soustraire $1$ au résultat et on a bien une bijection.

Le poids d’Hamming d’une chaîne n’est évidemment pas une fonction injective, en effet $w(01)=w(10)=1$. Elle est par contre bijective car pour tout entier $n$ on peut trouver une chaîne de caractères contenant $n$ bits égaux à $1$ (on peut prendre, par exemple, l’écriture de $2^n-1$ en base $2$).

L’image réciproque $w^{-1}(3)$ est constitué de tous les mots contenant exactement $3$ bits égaux à $1$. Cet ensemble est évidemment infini, mais son intersection avec $w^{-1}(5)$ est bien évidemment vide car aucun mot peut contenir à la fois exactement $3$ et $5$ bits à $1$. Donc $w^{-1}(3)\cap w^{-1}(5)=\emptyset$.

La relation $x\mathcal{S}y\Leftarrow\delta_1(x)=\delta_3(x)$ n’est ni réflexive, ni symétrique ni transitive. En effet

• $\delta_1(100) \ne\delta_3(100)$,
• $\delta_1(111)=\delta_3(100)$, mais $\delta_1(100)\ne\delta_3(111)$,
• $\delta_1(111)=\delta_3(100), \delta_1(100)=\delta_3(000)$, mais $\delta_1(111)\ne\delta_3(000)$.

La relation $x\mathcal{U}y\Leftrightarrow\exists i.\delta_i(x)=\delta_2(y)$ n’est ni symétrique, ni transitive. En effet

• $\delta_i(01) = \delta_2(11)$ en choisissant $i=1$, mais par contre $\delta_i(11)\ne\delta_2(01)$ pour tout $i$,
• $\delta_i(11) = \delta_2(10)$ en choisissant $i=1$ ou $i=2$, $\delta_i(10)=\delta_2(01)$ en choisissant $i=1$, mais $\delta_i(11)\ne\delta_2(01)$ pour tout $i$.

Par contre elle est évidemment réflexive car pour tout $x$ on a $\delta_i(x)=\delta_2(x)$ en choisissant $i=2$.

La relation $x\mathcal{T}y\Leftrightarrow w(x)=w(y)$ est une relation d’équivalence. La vérification est immédiate. Donc la classe d’équivalence de $x\in H$ par cette relation est constituée de toutes les chaînes contenant exactement le même nombre de $1$ que $x$. Par conséquent, $\overline{0110}\cap H_n$ est l’ensemble de toutes les chaînes contenant $2$ bits à $1$ et ayant longueur $n$. Alors

• $\overline{0110}\cap H_2 = \{11\}$,
• $\overline{0110}\cap H_3 = \{011,101,110\}$,
• $\overline{0110}\cap H_4 = \{0011,0101,0110,1001,1010,1100\}$.

Maintenant pour compter combien de chaînes de longueur $n$ ont exactement $2$ bits à $1$, on fixe le premier bit:

• S’il vaut $1$, les $n-1$ bits qui restent doivent contenir exactement un bit à $1$, et ce bit peut se trouver en chacune des $n-1$ positions. Il y a donc $n-1$ chaînes de cette forme.
• S’il vaut $0$, les $n-1$ bits qui restent doivent contenir exactement $2$ bits à $1$. Il y a donc $C(n-1)$ chaînes de cette forme.

En conclusion, $C(n)=C(n-1)+(n-1)$ et $C(2)=1$. On peut maintenant prouver la formule explicite par induction: on suppose $C(n)=n(n-1)/2$ pour un certain $n$, alors

$$C(n+1) = C(n) + n = \frac{n(n-1)}{2} + n = \frac{n^2+n}{2} = \frac{(n+1)n}{2}.$$