An element of a finite field. More...

Public Member Functions
Constructors
	FieldElement () throw ()
	Construct the special 0 element.
Properties
const Field< T > &	parent () const throw (UndefinedFieldException)
	The parent field.
Copy
You can copy elements using assignment.
	FieldElement (const FieldElement< T > &e) throw ()
FieldElement< T > &	operator= (const FieldElement< T > &e) throw ()
FieldElement< T > &	operator= (const BigInt &i) throw (UndefinedFieldException)
	Assign a scalar value to this element.
Binary operators
All binary operators throw a NotInSameFieldException if neither of this two conditions is satisfied: the two operands have the same parent field, the parent field of one operand is the prime field of the other's.
FieldElement< T >	operator+ (const FieldElement< T > &e) const throw (NotInSameFieldException)
FieldElement< T >	operator- (const FieldElement< T > &e) const throw (NotInSameFieldException)
FieldElement< T >	operator* (const FieldElement< T > &e) const throw (NotInSameFieldException)
FieldElement< T >	operator/ (const FieldElement< T > &e) const throw (NotInSameFieldException, DivisionByZeroException)
void	operator+= (const FieldElement< T > &) throw (NotInSameFieldException)
void	operator-= (const FieldElement< T > &) throw (NotInSameFieldException)
void	*operator=** (const FieldElement< T > &) throw (NotInSameFieldException)
void	operator/= (const FieldElement< T > &) throw (NotInSameFieldException, DivisionByZeroException)
void	sum (const FieldElement< T > &a, const FieldElement< T > &b) throw (NotInSameFieldException)
	Stores a + b in this element.
void	difference (const FieldElement< T > &a, const FieldElement< T > &b) throw (NotInSameFieldException)
	Stores a - b in this element.
void	product (const FieldElement< T > &a, const FieldElement< T > &b) throw (NotInSameFieldException)
	Stores a * b in this element.
void	division (const FieldElement< T > &a, const FieldElement< T > &b) throw (NotInSameFieldException, DivisionByZeroException)
	Stores a / b in this element.
Unary operators
FieldElement< T >	operator- () const throw ()
	Additive inverse.
FieldElement< T >	inv () const throw (DivisionByZeroException)
	Multiplicative inverse.
FieldElement< T >	operator^ (const ZZ &i) const throw ()
	Power.
FieldElement< T >	operator^ (const long i) const throw ()
	Power.
FieldElement< T >	frobenius () const throw ()
	p-th power (frobenius morphism).
FieldElement< T >	frobenius (const long n) const throw ()
	pⁿ-th power (iterated frobenius morphism).
FieldElement< T >	trace (const Field< T > &F) const throw (NotASubFieldException)
	Trace over the field F.
FieldElement< T >	trace () const throw ()
	Trace over F_p
FieldElement< T >	pseudotrace (unsigned long n) const throw ()
	n-th pseudotrace
Self-incrementing Unary operations
These operators store the result of the operation into the element itself.
void	negate () throw ()
	Flip the sign of this element.
void	self_inv () throw (DivisionByZeroException)
	Invert this element.
void	operator^= (const ZZ &) throw ()
	Power.
void	operator^= (const long) throw ()
	Power.
void	self_frobenius () throw ()
	p-th power (frobenius morphism).
void	self_frobenius (long) throw ()
	pⁿ-th power (iterated frobenius morphism).
void	self_trace (const Field< T > &F) throw (NotASubFieldException)
	Trace over the field F.
void	self_trace () throw ()
	Trace over F_p
void	self_pseudotrace (unsigned long) throw ()
	n-th pseudotrace
Minimal polynomials and Evaluation
FieldPolynomial< T >	minimalPolynomial () const throw ()
	The minimal polynomial over F_p.
FieldPolynomial< T >	minimalPolynomial (const Field< T > &F) const throw (NotASubFieldException, NotSupportedException)
	The minimal polynomial over the field F.
void	minimalPolynomials (const Field< T > &F, vector< FieldPolynomial< T > > &res) const throw (NotASubFieldException, NotSupportedException)
	All the minimal polynomials up to the field F.
FieldPolynomial< T >	affineMinimalPolynomial (const Field< T > &F, const FieldElement< T > &a, vector< FieldPolynomial< T > > &minpols) const throw (NotASubFieldException, NoSuchPolynomialException, NotSupportedException, BadParametersException)
	The a-affine minimal polynomial over the field F.
FieldPolynomial< T >	affineMinimalPolynomial (const Field< T > &F, const FieldElement< T > &a) const throw (NotASubFieldException, NoSuchPolynomialException, NotSupportedException)
	The a-affine minimal polynomial over the field F.
FieldElement< T >	evaluate (const FieldPolynomial< T > &P, vector< FieldPolynomial< T > > &minpols) const throw (IllegalCoercionException, BadParametersException)
	The evaulation of P at this element.
FieldElement< T >	evaluate (const FieldPolynomial< T > &P) const throw (IllegalCoercionException)
	The evaulation of P at this element.
Coercion of elements
Every element has an unique parent field, but it may belong to some subfield of its parent field or you may want to change its parent field to an overfield of its actual one. Coercion does exactly this. When the coericion is impossible because either there is no known embedding between the two fields or because the element does not belong to the new field, an IllegalCoercionException is thrown.
FieldElement< T >	toScalar () const throw (IllegalCoercionException)
	Coerce to a scalar.
FieldElement< T >	operator>> (const Field< T > &F) const throw (IllegalCoercionException)
	Coerce to the field F.
void	operator>>= (const Field< T > &) throw (IllegalCoercionException)
	Coerce to the field F and store the result in this element.
bool	isCoercible (const Field< T > &) const throw ()
	Test if this element is coercible to F.
Predicates
bool	operator== (const FieldElement< T > &) const throw (NotInSameFieldException)
	Equality.
bool	operator== (const BigInt &) const throw ()
	Equality.
bool	operator!= (const FieldElement< T > &e) const throw (NotInSameFieldException)
	Inequality.
bool	operator!= (const BigInt &i) const throw ()
	Inequality.
bool	isZero () const throw ()
	Test to zero.
bool	isOne () const throw ()
	Test to one.
bool	isScalar () const throw ()
	Test if this element belongs to F_p.
Access to the Infrastructure
These methods let you access the internal `NTL` representation of elements. Warning These methods are for advanced use only. Use them if you want to use an algorithm by you or in NTL that is not available for FieldElement.
void	toInfrastructure (GFp &e) const throw (IllegalCoercionException)
	Get the representation of elements whose parent field is F_p.
void	toInfrastructure (GFpE &e) const throw (IllegalCoercionException)
	Get the representation of elements whose parent field is an extension field.
Printing
ostream &	print (ostream &o) const
	Print this element to o.
ostream &	print (ostream &o, const string &var) const
	Print this element to o as a polynomial over F_p in the variable var.
ostream &	print (ostream &o, const vector< string > &vars) const
	Print this element to o as a multivariate polynomial over F_p.

Related Functions
(Note that these are not member functions.)
void	pushDown (const FieldElement< T > &e, vector< FieldElement< T > > &v) throw (NoSubFieldException)
	Convert e from the internal (univariate) representation to the bivariate representation over the immediate subfield in the primitive tower (the stem).
void	liftUp (const vector< FieldElement< T > > &v, FieldElement< T > &e) throw (NotInSameFieldException, NoOverFieldException)
	Convert v from the bivariate representation over the immediate subfield in the primitive tower (the stem) to the internal (univariate) representation.
template<class T >
ostream &	operator<< (ostream &o, const FieldElement< T > &e)
	Print e to o.

Local types
Local types defined in this class. They are aliases to simplify the access to the Infrastructure T and its subtypes. See Also Infrastructures.
typedef T	Infrastructure
typedef T::GFp	GFp
typedef T::MatGFp	MatGFp
typedef T::GFpX	GFpX
typedef T::GFpE	GFpE
typedef T::GFpEX	GFpEX
typedef T::BigInt	BigInt
typedef T::Context	Context

Detailed Description

template<class T>
class FAAST::FieldElement< T >

An element of a finite field.

Objects of this class represent elements of a finite field, as represented by the class Field. With the exception of the zero element created by the default constructor, any element has an unique parent field and binary operations can combine two elements only in one of the following two cases:

the two elements have the same parent field,
the parent element of one element is the prime field of the other's.

Elements created through the default constructor, as for example

FieldElement<T> elt;

have a special status as they don't belong to any specific field: their default value is 0 and they can be combined with any other element. The result of a binary operation involving such a special element is one of the following:

A DivisionByZeroException if the operation is division and the divisor is the special 0 element.
An element of field K, if K is the parent field of the other element.
The special 0 element if the other element is the special 0 element.
An UndefinedFieldException if the other element is not the special 0 element and yet does not belong to any field, as in this example
FieldElement<T> elt;

return elt + 1;

See UndefinedFieldException for more details.

Elements are internally represented as univariate polynomials with coefficients in F_p modulo an irreducible polynomial as described in [DFS '09, Section 3]. The way the arithmetics of the field are actually implemented is given by the template parameter T that must be one of the Infrastructures. Note that changing the Infrastructure may sensibly change the speed of your code.

Template Parameters

T	An Infrastructure. It specfies which `NTL` types will carry out the arithmetic operations.

See Also: Field, UndefinedFieldException

Examples:: test.c++, testIso.c++, testLE.c++, testStem.c++, testTraceFrob.c++, and using_infrastructure.c++.

Constructor & Destructor Documentation

template<class T>

FAAST::FieldElement< T >::FieldElement ( ) throw ()

inline

Construct the special 0 element.

The special 0 element does not belong to any field, yet it can be added, multiplied, etc. to any other FieldElement. See the introduction for more details. If you want to construct the 0 element of a specific field, use Field::zero() instead.

See Also: UndefinedFieldException, Field::zero().

Member Function Documentation

template<class T >

FieldPolynomial< T > FAAST::FieldElement< T >::affineMinimalPolynomial	(	const Field< T > &	F,
		const FieldElement< T > &	a,
		vector< FieldPolynomial< T > > &	minpols
	)		const throw (NotASubFieldException, NoSuchPolynomialException, NotSupportedException, BadParametersException)

The a-affine minimal polynomial over the field F.

This is an optimized version of affineMinimalPolynomial(const Field<T>&, const FieldElement<T>&) const that lets you pass an additional parameter minpols containing some precomputed quantities.

The optional parameter minpols must contain either the result of minimalPolynomials(F,minpols) , or must be an empty vector, in which case it is filled with the result of minimalPolynomials(F,minpols) . In any other case either a BadParametersException is thrown or the behaviour is undefined.

This method should be preferred when you care about efficiency and you do many calls to affineMinimalPolynomial() and evaluate().

Parameters

[in]	F	A subfield of the parent field.
[in]	a	An element contained in the field F[x], where x is this element.
[in,out]	minpols	If this vector is empty, then `minimalPolynomials(F,minpols)` is called, otherwise it is assumed to contain the data computed by the former method call.

Returns: The a-affine minimal polynomial over the field F.

Exceptions

NotASubFieldException	If the parent field is not an extension field of F.
NotSupportedException	If F is a prime field not being the base field of an Artin-Schreier tower.
NoSuchPolynomialException	If no such polynomial exists. Equivalently, if a is not an element of F[x] where x is this element.
BadParametersException	If minpols is not empty or does not contain the result of `minimalPolynomials(F,minpols)` .

See Also: affineMinimalPolynomial(const Field<T>&, const FieldElement<T>&) const.

Examples:: test.c++.

template<class T>

FieldPolynomial<T> FAAST::FieldElement< T >::affineMinimalPolynomial	(	const Field< T > &	F,
		const FieldElement< T > &	a
	)		const throw (NotASubFieldException, NoSuchPolynomialException, NotSupportedException)

inline

The a-affine minimal polynomial over the field F.

That is the minimum degree polynomial P of F[X] such that

$P(x) = \mathtt{a}\mathrm{,}$

where x is this element. Observe that this is the same as computing the interpolation polynomial such that

$P\bigl(\phi_F^n(x)\bigr) = \phi_F^n(\mathtt{a}) \quad \forall n\mathrm{,}$

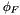where $\phi_F$ is the frobenius morphism fixing F. This implements a yet unpublished algorithm, it only works when F is a field of an Artin-Schreier tower as constructed in [DFS '09, Section 3].

Parameters

[in]	F	A subfield of the parent field.
[in]	a	An element contained in the field F[x], where x is this element.

Returns: The a-affine minimal polynomial over the field F.

Exceptions

NotASubFieldException	If the parent field is not an extension field of F.
NotSupportedException	If F is a prime field not being the base field of an Artin-Schreier tower.
NoSuchPolynomialException	If no such polynomial exists. Equivalently, if a is not an element of the field F[x], where x is this element. `minimalPolynomials(F,minpols)` .

template<class T >

FieldElement< T > FAAST::FieldElement< T >::evaluate	(	const FieldPolynomial< T > &	P,
		vector< FieldPolynomial< T > > &	minpols
	)		const throw (IllegalCoercionException, BadParametersException)

The evaulation of P at this element.

This is an optimized version of evaluate(const FieldPolynomial<T>&) const that lets you pass an additional parameter minpols containing some precomputed quantities.

The optional parameter minpols must contain either the result of minimalPolynomials(F,minpols) , or must be an empty vector, in which case it is filled with the result of minimalPolynomials(F,minpols) . In any other case either a BadParametersException is thrown or the behaviour is undefined.

This method should be preferred when you care about efficiency and you do many calls to affineMinimalPolynomial() and evaluate().

Parameters

[in]	P	A polynomial with coefficients in a subfield or overfield of the parent field.
[in,out]	minpols	If this vector is empty, then `minimalPolynomials(F,minpols)` is called, otherwise it is assumed to contain the data computed by the former method call.

Returns: The evaluation of P at this element.

Exceptions

IllegalCoercionException	If this element cannot be coerced to the coefficient field of P nor can P be coerced to the parent field.
BadParametersException	If minpols is not empty or does not contain the result of `minimalPolynomials(F,minpols)` .

Invariant: This is the same as P.evaluate(*this, minpols) .

See Also: evaluate(const FieldPolynomial<T>&) const, FieldPolynomial::evaluate().

Examples:: test.c++.

template<class T>

FieldElement<T> FAAST::FieldElement< T >::evaluate ( const FieldPolynomial< T > & P ) const throw (IllegalCoercionException)

inline

The evaulation of P at this element.

This implements a yet unpublished algorithm for Artin-Schreier towers constructed as in [DFS '09, Section 3]. It uses Horner evaluation scheme for all the other cases.

The optional parameter minpols must contain either the result of this.minimalPolynomials(P.parent,v), or must be an empty vector, in which case it is filled with the result of minimalPolynomials(P.parent,v).

Parameters

[in] P A polynomial with coefficients in a subfield or overfield of the parent field.

Returns: The evaluation of P at this element.

Exceptions

IllegalCoercionException If this element cannot be coerced to the coefficient field of P nor can P be coerced to the parent field.

Invariant: This is the same as P.evaluate(*this) .

See Also: FieldPolynomial::evaluate().

template<class T>

FieldElement<T> FAAST::FieldElement< T >::frobenius ( const long n ) const throw ()

inline

pⁿ-th power (iterated frobenius morphism).

This method is a generalization of the algorithm IterFrobenius of [DFS '09, Section 5].

template<class T >

bool FAAST::FieldElement< T >::isScalar ( ) const throw ()

Test if this element belongs to F_p.

See Also: toScalar().

template<class T>

FieldPolynomial<T> FAAST::FieldElement< T >::minimalPolynomial ( const Field< T > & F ) const throw (NotASubFieldException, NotSupportedException)

inline

The minimal polynomial over the field F.

This method implements a yet unpublished algorithm to compute minimal polynomials in Artin-Schreier towers. It only works when F is a field of an Artin-Schreier tower as constructed in [DFS '09, Section 3].

Parameters

[in] F A subfield of the parent field of this element.

Returns: A polynomial over F being the minimal polynomial of this element.

Exceptions

NotASubFieldException	If the parent field is not an extension field of F.
NotSupportedException	If F is a prime field not being the base field of an Artin-Schreier tower. Use minimalPolynomial() instead.

template<class T >

void FAAST::FieldElement< T >::minimalPolynomials	(	const Field< T > &	F,
		vector< FieldPolynomial< T > > &	res
	)		const throw (NotASubFieldException, NotSupportedException)

All the minimal polynomials up to the field F.

The result is the same as doing

res[0] = minimalPolynomial(F);
res[1] = minimalPolynomial(F.overField());
res[2] = minimalPolynomial(F.overField().overField());
...

up to minimalPolynomial(parent()). The computation is more efficient, though.

Parameters

[in]	F	A subfield of the parent field field.
[out]	res	The vector is filled with the minimal polynomials of this element over the intermediate extension fields of F. All previous data are discarded.

Exceptions

NotASubFieldException	If the parent field is not an extension field of F.
NotSupportedException	If F is a prime field not being the base field of an Artin-Schreier tower. Use minimalPolynomial() instead.

See Also: minimalPolynomial(const Field<T>&) const.

Examples:: test.c++.

template<class T>

bool FAAST::FieldElement< T >::operator!= ( const FieldElement< T > & e ) const throw (NotInSameFieldException)

inline

Inequality.

This method does not try to coerce the elements to the same field to test equality.

Exceptions

NotInSameFieldException If the two elements do not have de same parent field.

template<class T >

FieldElement< T > & FAAST::FieldElement< T >::operator= ( const BigInt & i ) throw (UndefinedFieldException)

Assign a scalar value to this element.

The parent field of the element does not change through the assignment.

Returns: A reference to the result.

Exceptions

UndefinedFieldException If this is the special 0 element and i is different from 0.

template<class T >

bool FAAST::FieldElement< T >::operator== ( const FieldElement< T > & e ) const throw (NotInSameFieldException)

Equality.

This method does not try to coerce the elements to the same field to test equality.

Exceptions

NotInSameFieldException If the two elements do not have de same parent field.

template<class T>

FieldElement<T> FAAST::FieldElement< T >::operator>> ( const Field< T > & F ) const throw (IllegalCoercionException)

inline

Coerce to the field F.

Parameters

[in] F A finite subfield or overfield of the parent field, containing this element.

Returns: The newly created element.

Exceptions

IllegalCoercionException If no embedding is known between the parent field and F or if this element does not belong to F.

template<class T >

void FAAST::FieldElement< T >::operator>>= ( const Field< T > & F ) throw (IllegalCoercionException)

Coerce to the field F and store the result in this element.

Parameters

[in] F A finite subfield or overfield of the parent field, containing this element.

Exceptions

IllegalCoercionException If no embedding is known between the parent field and F or if this element does not belong to F.

template<class T>

const Field<T>& FAAST::FieldElement< T >::parent ( ) const throw (UndefinedFieldException)

inline

The parent field.

With the exception of the zero element created by the default constructor, any element has an unique parent field and binary operations can combine two elements only in one of the following two cases:

the two elements have the same parent field,
the parent element of one element is the prime field of the other's.

Exceptions

UndefinedFieldException If this element does not belong to any field.

See Also: FieldElement(), UndefinedFieldException.

template<class T >

ostream & FAAST::FieldElement< T >::print	(	ostream &	o,
		const vector< string > &	vars
	)		const

Print this element to o as a multivariate polynomial over F_p.

The number of variables in vars must be at least one plus the Artin-Schreier height of the parent field. The recursive descent along the tower is done via Field::toBivariate(), the list of the fields involved in the descent is internally stored and reproduces backwards the list of calls to Field::ArtinSchreierExtension that have created the parent field.

Parameters

[in,out]	o	An output stream.
[in]	vars	A vector of variable names.

Returns: A pointer to the modified stream.

Exceptions

BadParametersException If there is not enough variables in vars.

Todo:: This method sucks!

template<class T>

FieldElement<T> FAAST::FieldElement< T >::pseudotrace ( unsigned long n ) const throw ()

inline

n-th pseudotrace

Let x be this element, the n-th pseudotrace, noted T_n(x) is

$\mathrm{T}_n(x) = \sum_{\ell=0}^{n-1} x^{p^\ell} \mathrm{.}$

This method is a generalization of the algorithm Pseudotrace of [DFS '09, Section 5].

Examples:: testTraceFrob.c++.

template<class T >

void FAAST::FieldElement< T >::self_pseudotrace ( unsigned long n ) throw ()

n-th pseudotrace

Let x be this element, the n-th pseudotrace, noted T_n(x) is

$\mathrm{T}_n(x) = \sum_{\ell=0}^{n-1} x^{p^\ell} \mathrm{.}$

This method is a generalization of the algorithm Pseudotrace of [DFS '09, Section 5].

template<class T >

void FAAST::FieldElement< T >::toInfrastructure ( GFp & e ) const throw (IllegalCoercionException)

Get the representation of elements whose parent field is F_p.

Parameters

[out] e An NTL scalar element to hold the result.

Exceptions

IllegalCoercionException If the parent field is not a prime field

Note: This method automatically switches the context to the parent field context. See Field::switchContext().

See Also: using_infrastructure.c++ , Field::fromInfrastructure(), Field::switchContext().

template<class T >

void FAAST::FieldElement< T >::toInfrastructure ( GFpE & e ) const throw (IllegalCoercionException)

Get the representation of elements whose parent field is an extension field.

Parameters

[out] e An NTL element to hold the result.

Exceptions

IllegalCoercionException If the parent field is a prime field

Note: This method automatically switches the context to the parent field context. See Field::switchContext().

See Also: using_infrastructure.c++ , Field::fromInfrastructure(), Field::switchContext().

template<class T >

FieldElement< T > FAAST::FieldElement< T >::toScalar ( ) const throw (IllegalCoercionException)

Coerce to a scalar.

Coerce to an element of F_p.

Returns: The newly created element.

Exceptions

IllegalCoercionException If the element is not a scalar.

Invariant: This is the same as doing
*this >> parent().primeField();

template<class T>

FieldElement<T> FAAST::FieldElement< T >::trace ( const Field< T > & F ) const throw (NotASubFieldException)

inline

Trace over the field F.

Exceptions

NotASubFieldException If this element does not belong to an overfield of F.

Examples:: testIso.c++.

Friends And Related Function Documentation

template<class T>

void liftUp	(	const vector< FieldElement< T > > &	v,
		FieldElement< T > &	e
	)		throw (NotInSameFieldException, NoOverFieldException)

friend

Convert v from the bivariate representation over the immediate subfield in the primitive tower (the stem) to the internal (univariate) representation.

If the parent field of the elements of v is the prime field, then e is the element whose univariate representation has v as cofficients. Otherwise let

x = v[0].parent().primitiveElement();

This method stores in e an element of e.parent().overField() such that

$\begin{equation} \mathtt{e} = \mathtt{v[0]} + \mathtt{v[1]}*\mathtt{x} + ... + \mathtt{v[p-1]}*\mathtt{x}^{p-1} \mathrm{,} \end{equation}$

If v is too short, it is filled with zeros. If v is too long, the unnecessary elements are ignored.

Let K be the field in the primitive tower (the stem) isomorphic to the parent field of the elements of v, this corresponds to convert v from the multivariate representation as an element of K[x] to the internal (univariate) representation. This routine implements the algorithm LiftUp of [DFS '09, Section 4.4].

Parameters

[in]	v	A vector of elements all in the same field.
[out]	e	An element satisfying condition (2).

Exceptions

NotInSameFieldException	If the elements of v do not all have the same parent field.
NoOverFieldException	If the parent field of the elements of v has no overfield.

Note: The result always lies in the primitive tower (the stem), even if the elements of v do not.

Invariant: If the parent field of the elements of v is in the primitive tower (the stem), this is equivalent to
v[0].parent().overField().toUnivariate(e, v);

and this latter form should be preferred for the sake of clarity.

See Also: Field::toUnivariate().

template<class T>

void pushDown	(	const FieldElement< T > &	e,
		vector< FieldElement< T > > &	v
	)		throw (NoSubFieldException)

friend

Convert e from the internal (univariate) representation to the bivariate representation over the immediate subfield in the primitive tower (the stem).

If the parent field of e is the base field of an Artin-Schreier tower, then v is filled with the coefficients in F_p of its univariate representation. Otherwise let

x = e.parent().primitiveElement();

This method fills the vector v with p elements of e.parent().subField() such that

$\begin{equation} \mathtt{e} = \mathtt{v[0]} + \mathtt{v[1]}*\mathtt{x} + ... + \mathtt{v[p-1]}*\mathtt{x}^{p-1} \mathrm{.} \end{equation}$

Let K be the field in the primitive tower (the stem) isomorphic to e.parent().subField() , this corresponds to convert e from its internal (univariate) representation to the bivariate representation as an element of K[x]. This routine implements the algorithm PushDown of [DFS '09, Section 4.2].

Parameters

[in]	e	An element of any field.
[out]	v	A vector of elements of `e.parent().stemField()` that satisfies condition (1).

Exceptions

NoSubFieldException If F_p is the parent field of e.

Note: The result always lies in the primitive tower (the stem), even if e does not.

Invariant: If the parent field of e is in the primitive tower (the stem), this is equivalent to
e.parent().subField().toBivariate(e, v);

and this latter form should be preferred for the sake of clarity.

See Also: Field::toBivariate().

Public Member Functions

Related Functions

Local types

Detailed Description

template<class T> class FAAST::FieldElement< T >

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

template<class T>
class FAAST::FieldElement< T >