An polynomial with coefficients over a finite field. More...

Public Member Functions
Constructors
	FieldPolynomial () throw ()
	Construct the special 0 polynomial.
Properties
const Field< T > &	parent () const throw (UndefinedFieldException)
	The parent field.
long	degree () const throw ()
	Degree of the polynomial.
Copy
You can copy polynomials using assignment.
	FieldPolynomial (const FieldPolynomial< T > &) throw ()
FieldPolynomial< T > &	operator= (const FieldPolynomial< T > &) throw ()
	FieldPolynomial (const FieldElement< T > &e) throw ()
FieldPolynomial< T > &	operator= (const FieldElement< T > &e) throw ()
FieldPolynomial< T > &	operator= (const BigInt &i) throw (UndefinedFieldException)
	The degree 0 polynomial with constant coefficient i.
Access to coefficients
void	getCoeff (const long i, FieldElement< T > &e) const throw (BadParametersException)
	Store in e the i-th coefficient.
void	setCoeff (const long i, const FieldElement< T > &e) throw (NotInSameFieldException, BadParametersException)
	Set the i-th coefficient to e.
void	setCoeff (const long i, const BigInt &c) throw (UndefinedFieldException, BadParametersException)
	Set the i-th coefficient to c.
void	setCoeff (const long i) throw (UndefinedFieldException, BadParametersException)
	Set the i-th coefficient to 1.
Binary operators
All binary operators throw a NotInSameFieldException if neither of this two conditions is satisfied: the two operands have the same parent field, the parent field of one operand is the prime field of the other's.
FieldPolynomial< T >	operator+ (const FieldPolynomial< T > &e) const throw (NotInSameFieldException)
FieldPolynomial< T >	operator- (const FieldPolynomial< T > &e) const throw (NotInSameFieldException)
FieldPolynomial< T >	operator* (const FieldPolynomial< T > &e) const throw (NotInSameFieldException)
FieldPolynomial< T >	operator/ (const FieldPolynomial< T > &e) const throw (NotInSameFieldException, DivisionByZeroException)
FieldPolynomial< T >	operator% (const FieldPolynomial< T > &e) const throw (NotInSameFieldException, DivisionByZeroException)
FieldPolynomial< T >	operator<< (const long n) const
	Left shift.
FieldPolynomial< T >	operator>> (const long n) const
	Right shift.
void	operator+= (const FieldPolynomial< T > &) throw (NotInSameFieldException)
void	operator-= (const FieldPolynomial< T > &) throw (NotInSameFieldException)
void	*operator=** (const FieldPolynomial< T > &) throw (NotInSameFieldException)
void	operator/= (const FieldPolynomial< T > &) throw (NotInSameFieldException, DivisionByZeroException)
void	operator%= (const FieldPolynomial< T > &) throw (NotInSameFieldException, DivisionByZeroException)
void	operator<<= (const long n)
	Left shift.
void	operator>>= (const long n)
	Right shift.
void	sum (const FieldPolynomial< T > &a, const FieldPolynomial< T > &b) throw (NotInSameFieldException)
	Stores a + b in this polynomial.
void	difference (const FieldPolynomial< T > &a, const FieldPolynomial< T > &b) throw (NotInSameFieldException)
	Stores a - b in this polynomial.
void	product (const FieldPolynomial< T > &a, const FieldPolynomial< T > &b) throw (NotInSameFieldException)
	Stores a * b in this polynomial.
void	division (const FieldPolynomial< T > &a, const FieldPolynomial< T > &b) throw (NotInSameFieldException, DivisionByZeroException)
	Stores a / b in this polynomial.
void	mod (const FieldPolynomial< T > &a, const FieldPolynomial< T > &b) throw (NotInSameFieldException, DivisionByZeroException)
	Stores a % b in this polynomial.
void	LeftShift (const FieldPolynomial< T > &a, const long n)
	Left shift. Stores a * Xⁿ in this polynomial.
void	RightShift (const FieldPolynomial< T > &a, const long n)
	Right shift. Stores a / Xⁿ in this polynomial.
Unary operators
bool	divides (const FieldPolynomial< T > &P) const throw ()
	Test divisibility of this polynomial by P.
FieldPolynomial< T >	operator- () const throw ()
FieldPolynomial< T >	operator^ (const long i) const throw ()
	Power.
FieldPolynomial< T >	derivative () const throw ()
FieldPolynomial< T >	monic () const throw ()
	The monic polynomial obtained by dividing this polynomial by its leading coeffcient.
FieldPolynomial< T >	frobenius () const throw ()
	p-th power (frobenius morphism) of the coefficients.
FieldPolynomial< T >	frobenius (const long n) const throw ()
	pⁿ-th power (iterated frobenius morphism) of the coefficients.
Self-incrementing Unary operations
These operators store the result of the operation into the polynomial itself.
void	negate () throw ()
	Flip the sign of this polynomial.
void	operator^= (const long) throw ()
	Power.
void	self_derivative () throw ()
	Derivative.
void	normalize () throw ()
	Make this polynomial monic.
void	self_frobenius () throw ()
	p-th power (frobenius morphism) of the coefficients.
void	self_frobenius (long) throw ()
	pⁿ-th power (iterated frobenius morphism) of the coefficients.
Coercion of polynomials
Every polynomial has an unique parent field, but its coefficients may belong to some subfield of its parent field or you may want to change its parent field to an overfield of its actual one. Coercion does exactly this. When the coericion is impossible because either there is no known embedding between the two fields or because the coefficients do not belong to the new field, an IllegalCoercionException is thrown.
FieldPolynomial< T >	toScalarPolynomial () const throw (IllegalCoercionException)
	Coerce to a scalar polynomial.
FieldPolynomial< T >	operator>> (const Field< T > &) const throw (IllegalCoercionException)
	Coerce to the field F.
void	operator>>= (const Field< T > &F) throw (IllegalCoercionException)
	Coerce to the field F and store the result in this polynomial.
bool	isCoercible (const Field< T > &) const throw ()
	Test if this polynomial is coercible to F.
Evaluation
FieldElement< T >	evaluate (const FieldElement< T > &e, vector< FieldPolynomial< T > > &minpols) const throw (IllegalCoercionException, BadParametersException)
	The evaulation of this polynomial at e.
FieldElement< T >	evaluate (const FieldElement< T > &e) const throw (IllegalCoercionException, BadParametersException)

Predicates
bool	operator== (const FieldPolynomial< T > &) const throw (NotInSameFieldException)
	Equality.
bool	operator== (const FieldElement< T > &) const throw (NotInSameFieldException)
	Equality.
bool	operator== (const BigInt &) const throw ()
	Equality.
bool	operator!= (const FieldPolynomial< T > &e) const throw (NotInSameFieldException)
	Inequality.
bool	operator!= (const FieldElement< T > &e) const throw (NotInSameFieldException)
	Inequality.
bool	operator!= (const BigInt &i) const throw ()
	Inequality.
bool	isZero () const throw ()
	Test to zero.
bool	isOne () const throw ()
	Test to one.
bool	isScalarPolynomial () const throw ()
	Test if this polynomial has coefficients in F_p.
Access to the Infrastructure
These methods let you access the internal `NTL` representation of polynomials. Warning These methods are for advanced use only. Use them if you want to use an algorithm by you or in NTL that is not available for FieldPolynomial.
void	toInfrastructure (GFpX &P) const throw (IllegalCoercionException)
	Get the representation of polynomials whose parent field is F_p.
void	toInfrastructure (GFpEX &P) const throw (IllegalCoercionException)
	Get the representation of polynomials whose parent field is an extension field.
Printing
ostream &	print (ostream &) const
	Print this polynomial to o.
ostream &	print (ostream &, const string &varPoly, const string &varField) const
	Print this element to o as a polynomial over its parent field.
ostream &	print (ostream &, const string &varPoly, const vector< string > &varsField) const
	Print this element to o as a polynomial over its parent field.

Related Functions
(Note that these are not member functions.)
FieldPolynomial< T >	GCD (const FieldPolynomial< T > &P, const FieldPolynomial< T > &Q) throw (NotInSameFieldException)
	GCD of P and Q.
void	XGCD (const FieldPolynomial< T > &P, const FieldPolynomial< T > &Q, FieldPolynomial< T > &U, FieldPolynomial< T > &V, FieldPolynomial< T > &G) throw (NotInSameFieldException)
	XGCD of P and Q.
void	HalfGCD (FieldPolynomial< T > &U0, FieldPolynomial< T > &V0, FieldPolynomial< T > &U1, FieldPolynomial< T > &V1, const FieldPolynomial< T > &P, const FieldPolynomial< T > &Q, const long d) throw (NotInSameFieldException, BadParametersException)
	Half GCD of P and Q.
template<class T >
ostream &	operator<< (ostream &o, const FieldPolynomial< T > &P)
	Print P to o.

Local types
Local types defined in this class. They are aliases to simplify the access to the Infrastructure T and its subtypes. See Also Infrastructures.
typedef T	Infrastructure
typedef T::GFp	GFp
typedef T::MatGFp	MatGFp
typedef T::GFpX	GFpX
typedef T::GFpE	GFpE
typedef T::GFpEX	GFpEX
typedef T::BigInt	BigInt
typedef T::Context	Context

Detailed Description

template<class T>
class FAAST::FieldPolynomial< T >

An polynomial with coefficients over a finite field.

Objects of this class represent polynomials over a finite field, as represented by the class Field. With the exception of the zero polynomial created by the default constructor, any element has an unique parent field and binary operations can combine two elements only in one of the following two cases:

the two polynomials have the same parent field,
the parent element of one polynomial is the prime field of the other's.

Polynomials created through the default constructor, as for example

FieldPolynomial<T> P;

have a special status as they don't belong to any specific field: their default value is 0 and they can be combined with any other polynomial. The result of a binary operation involving such a special polynomial is one of the following:

A DivisionByZeroException if the operation is division and the divisor is the special 0 polynomial.
A polynomial over the field K, if K is the parent field of the other polynomial.
The special 0 polynomial if the other polynomial is the special 0 polynomial.
An UndefinedFieldException if the other polynomial is not the special 0 polynomial and yet does not belong to any field, as in this example
FieldPolynomial<T> P;

return P + 1;

See UndefinedFieldException for more details.

The way the arithmetics of the field are actually implemented is given by the template parameter T that must be one of the Infrastructures. Note that changing the Infrastructure may sensibly change the speed of your code.

Template Parameters

T	An Infrastructure. It specfies which `NTL` types will carry out the arithmetic operations.

See Also: Field, FieldElement, UndefinedFieldException

Examples:: test.c++.

Constructor & Destructor Documentation

template<class T>

FAAST::FieldPolynomial< T >::FieldPolynomial ( ) throw ()

inline

Construct the special 0 polynomial.

The special 0 polynomial has no coefficient field, yet it can be added, multiplied, etc. to any other FieldPolynomial. See the introduction for more details. If you want to construct the 0 polynomial of a specific field, use Field::zero() in conjunction with FieldPolynomial(const FieldElement<T>&) instead.

See Also: UndefinedFieldException, Field::zero(), FieldPolynomial(const FieldElement<T>&).

Member Function Documentation

template<class T >

long FAAST::FieldPolynomial< T >::degree ( ) const throw ()

Degree of the polynomial.

Returns: The degree of the polynomial or -1 if the polynomial is 0.

template<class T>

FieldElement<T> FAAST::FieldPolynomial< T >::evaluate	(	const FieldElement< T > &	e,
		vector< FieldPolynomial< T > > &	minpols
	)		const throw (IllegalCoercionException, BadParametersException)

inline

The evaulation of this polynomial at e.

See Also: FieldElement::evaluate(const FieldPolynomial<T>&, vector<FieldPolynomial<T> >&) const.

Examples:: test.c++.

template<class T>

FieldElement<T> FAAST::FieldPolynomial< T >::evaluate ( const FieldElement< T > & e ) const throw (IllegalCoercionException, BadParametersException)

inline

See Also: FieldElement::evaluate(const FieldPolynomial<T>&) const.

template<class T>

FieldPolynomial<T> FAAST::FieldPolynomial< T >::frobenius ( ) const throw ()

inline

p-th power (frobenius morphism) of the coefficients.

Apply the frobenius morphism to the coefficients of this polynomial.

See Also: FieldElement::frobenius().

template<class T>

FieldPolynomial<T> FAAST::FieldPolynomial< T >::frobenius ( const long n ) const throw ()

inline

pⁿ-th power (iterated frobenius morphism) of the coefficients.

Apply the iterated frobenius morphism to the coefficients of this polynomial.

See Also: FieldElement::frobenius(const long) const.

template<class T >

void FAAST::FieldPolynomial< T >::getCoeff	(	const long	i,
		FieldElement< T > &	e
	)		const throw (BadParametersException)

Store in e the i-th coefficient.

Parameters

[in]	i	A positive integer.
[out]	e	A FieldElement to hold the result.

Exceptions

BadParametersException If i is negative.

template<class T >

bool FAAST::FieldPolynomial< T >::isScalarPolynomial ( ) const throw ()

Test if this polynomial has coefficients in F_p.

See Also: toScalarPolynomial().

template<class T >

void FAAST::FieldPolynomial< T >::LeftShift	(	const FieldPolynomial< T > &	a,
		const long	n
	)

Left shift. Stores a * Xⁿ in this polynomial.

See Also: operator<<(const long) const .

template<class T >

void FAAST::FieldPolynomial< T >::normalize ( ) throw ()

Make this polynomial monic.

See Also: monic().

template<class T>

bool FAAST::FieldPolynomial< T >::operator!= ( const FieldPolynomial< T > & e ) const throw (NotInSameFieldException)

inline

Inequality.

This method does not try to coerce the polynomials to the same field to test equality.

Exceptions

NotInSameFieldException If the two polynomials do not have de same parent field.

template<class T>

FieldPolynomial<T> FAAST::FieldPolynomial< T >::operator<< ( const long n ) const

inline

Left shift.

Parameters

[in] n an integer.

Returns: The product of this polynomial by Xⁿ.

Invariant: P << n equals P >> -n.

template<class T>

void FAAST::FieldPolynomial< T >::operator<<= ( const long n )

inline

Left shift.

See Also: operator<<(const long) const

template<class T >

FieldPolynomial< T > & FAAST::FieldPolynomial< T >::operator= ( const BigInt & i ) throw (UndefinedFieldException)

The degree 0 polynomial with constant coefficient i.

The parent field of the polynomial does not change through the assignment.

Returns: A reference to the result.

Exceptions

UndefinedFieldException If this is the special 0 element and i is different from 0.

template<class T >

bool FAAST::FieldPolynomial< T >::operator== ( const FieldPolynomial< T > & e ) const throw (NotInSameFieldException)

Equality.

This method does not try to coerce the polynomials to the same field to test equality.

Exceptions

NotInSameFieldException If the two polynomials do not have de same parent field.

template<class T>

FieldPolynomial<T> FAAST::FieldPolynomial< T >::operator>> ( const long n ) const

inline

Right shift.

Parameters

[in] n an integer.

Returns: The quotient of this polynomial by Xⁿ.

Invariant: P >> n equals P << -n.

template<class T >

FieldPolynomial< T > FAAST::FieldPolynomial< T >::operator>> ( const Field< T > & F ) const throw (IllegalCoercionException)

Coerce to the field F.

Parameters

[in] F A finite subfield or overfield of the parent field, containing the coefficients of the polynomial.

Returns: The newly created polynomial.

Exceptions

IllegalCoercionException If no embedding is known between the parent field and F or if the coefficients do not belong to F.

template<class T>

void FAAST::FieldPolynomial< T >::operator>>= ( const long n )

inline

Right shift.

See Also: operator>>(const long) const

template<class T>

void FAAST::FieldPolynomial< T >::operator>>= ( const Field< T > & F ) throw (IllegalCoercionException)

inline

Coerce to the field F and store the result in this polynomial.

Parameters

[in] F A finite subfield or overfield of the parent field, containing the coefficients of the polynomial.

Exceptions

IllegalCoercionException If no embedding is known between the parent field and F or if the coefficients do not belong to F.

template<class T>

const Field<T>& FAAST::FieldPolynomial< T >::parent ( ) const throw (UndefinedFieldException)

inline

The parent field.

With the exception of the zero polynomial created by the default constructor, any polynomial has an unique parent field and binary operations can combine two polynomials only in one of the following two cases:

the two polynomials have the same parent field,
the parent element of one polynomial is the prime field of the other's.

Exceptions

UndefinedFieldException If this polynomial has no coefficient field.

See Also: FieldElement(), UndefinedFieldException.

template<class T >

ostream & FAAST::FieldPolynomial< T >::print	(	ostream &	o,
		const string &	varPoly,
		const string &	varField
	)		const

Print this element to o as a polynomial over its parent field.

Print as a polynomial in the variable varPoly and print elements of the parent field as polynomials over F_p in the variable varField. The coefficients of the polynomial are printed as through FieldElement::print(o,varField) .

Parameters

[in,out]	o	An output stream.
[in]	varPoly	A variable name.
[in]	varField	A variable name.

Returns: A pointer to the modified stream.

See Also: FieldElement::print(ostream&, const string&) const.

template<class T >

ostream & FAAST::FieldPolynomial< T >::print	(	ostream &	o,
		const string &	varPoly,
		const vector< string > &	varsField
	)		const

Print this element to o as a polynomial over its parent field.

Print as a polynomial in the variable varPoly and print elements of the parent field as multivariate polynomials over F_p in the variables varsField. The coefficients of the polynomial are printed as through FieldElement::print(o,varsField) .

Parameters

[in,out]	o	An output stream.
[in]	varPoly	A variable name.
[in]	varsField	A vector of variable names.

Returns: A pointer to the modified stream.

See Also: FieldElement::print(ostream&, const vector<string>&) const.

template<class T >

void FAAST::FieldPolynomial< T >::RightShift	(	const FieldPolynomial< T > &	a,
		const long	n
	)

Right shift. Stores a / Xⁿ in this polynomial.

See Also: operator>>(const long) const .

template<class T >

void FAAST::FieldPolynomial< T >::setCoeff	(	const long	i,
		const FieldElement< T > &	e
	)		throw (NotInSameFieldException, BadParametersException)

Set the i-th coefficient to e.

If this polynomial is the special 0 polynomial, its parent field becomes the parent field of e after this call. If moreover e is the special 0 element, this method does nothing.

Parameters

[in]	i	A positive integer.
[out]	e	A FieldElement having the same parent field as this polynomial or the special 0 element.

Exceptions

BadParametersException	If i is negative.
NotInSameFieldException	If the parent fields of e and this polynomial are both defined and differ.

template<class T >

void FAAST::FieldPolynomial< T >::setCoeff	(	const long	i,
		const BigInt &	c
	)		throw (UndefinedFieldException, BadParametersException)

Set the i-th coefficient to c.

Parameters

[in]	i	A positive integer.
[out]	c	An integer.

Exceptions

BadParametersException	If i is negative.
UndefinedFieldException	If this is the special 0 polynomial and c is different from 0.

template<class T >

void FAAST::FieldPolynomial< T >::setCoeff ( const long i ) throw (UndefinedFieldException, BadParametersException)

Set the i-th coefficient to 1.

Parameters

[in] i A positive integer.

Exceptions

BadParametersException	If i is negative.
UndefinedFieldException	If this is the special 0 polynomial.

template<class T >

void FAAST::FieldPolynomial< T >::toInfrastructure ( GFpX & P ) const throw (IllegalCoercionException)

Get the representation of polynomials whose parent field is F_p.

Parameters

[out] P An NTL scalar polynomial to hold the result.

Exceptions

IllegalCoercionException If the parent field is not a prime field

Note: This method automatically switches the context to the parent field context. See Field::switchContext().

See Also: using_infrastructure.c++ , Field::fromInfrastructure(), Field::switchContext().

template<class T >

void FAAST::FieldPolynomial< T >::toInfrastructure ( GFpEX & P ) const throw (IllegalCoercionException)

Get the representation of polynomials whose parent field is an extension field.

Parameters

[out] P An NTL polynomial to hold the result.

Exceptions

IllegalCoercionException If the parent field is a prime field

Note: This method automatically switches the context to the parent field context. See Field::switchContext().

See Also: using_infrastructure.c++ , Field::fromInfrastructure(), Field::switchContext().

template<class T >

FieldPolynomial< T > FAAST::FieldPolynomial< T >::toScalarPolynomial ( ) const throw (IllegalCoercionException)

Coerce to a scalar polynomial.

Coerce to a polynomial with coefficients in F_p.

Returns: The newly created polynomial.

Exceptions

IllegalCoercionException If the polynomial is not a scalar polynomial.

Invariant: This is the same as doing
*this >> parent().primeField();

Friends And Related Function Documentation

template<class T>

FieldPolynomial<T> GCD	(	const FieldPolynomial< T > &	P,
		const FieldPolynomial< T > &	Q
	)		throw (NotInSameFieldException)

friend

GCD of P and Q.

Exceptions

NotInSameFieldException If P and Q do not have the same parent field.

template<class T>

void HalfGCD	(	FieldPolynomial< T > &	U0,
		FieldPolynomial< T > &	V0,
		FieldPolynomial< T > &	U1,
		FieldPolynomial< T > &	V1,
		const FieldPolynomial< T > &	P,
		const FieldPolynomial< T > &	Q,
		const long	d
	)		throw (NotInSameFieldException, BadParametersException)

friend

Half GCD of P and Q.

Parameters

[out]	U0	A polynomial to hold the result.
[out]	V0	A polynomial to hold the result.
[out]	U1	A polynomial to hold the result.
[out]	V1	A polynomial to hold the result.
[in]	P	A polynomial.
[in]	Q	A polynomial having the same parent field as P.
[in]	d	A bound on the degree of the result.

Exceptions

NotInSameFieldException	If P and Q do not have the same parent field.
BadParametersException	If 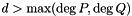$d>\max(\deg P,\deg Q)$ or .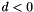

Invariant: at the end of the method the following relation holds:
$\left(\begin{array}{cc}U_0&V_0\\U_1&V_1\end{array}\right) \left(\begin{array}{c}P\\Q\end{array}\right) = \left(\begin{array}{c}R_j\\R_{j+1}\end{array}\right)$
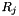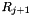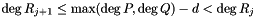where and $R_{j+1}$ are the reminders in the XGCD computation of P and Q such that $\deg R_{j+1}\le\max(\deg P,\deg Q)-d<\deg R_j$ .

template<class T>

void XGCD	(	const FieldPolynomial< T > &	P,
		const FieldPolynomial< T > &	Q,
		FieldPolynomial< T > &	U,
		FieldPolynomial< T > &	V,
		FieldPolynomial< T > &	G
	)		throw (NotInSameFieldException)

friend

XGCD of P and Q.

Parameters

[in]	P	A polynomial.
[in]	Q	A polynomial having the same parent field as P.
[out]	U	A polynomial to hold the result.
[out]	V	A polynomial to hold the result.
[out]	G	The GCD of this polynomial and Q.

Exceptions

NotInSameFieldException If P and Q do not have the same parent field.

Invariant: at the end of the method the following relation holds:
U*P + V*Q == G;

Public Member Functions

Related Functions

Local types

Detailed Description

template<class T> class FAAST::FieldPolynomial< T >

Constructor & Destructor Documentation

Member Function Documentation

Friends And Related Function Documentation

template<class T>
class FAAST::FieldPolynomial< T >