A finite field. More...

Public Member Functions
Artin-Schreier Extensions
Build Artin-Schreier extensions as described in [DFS '09].
const Field< T > &	ArtinSchreierExtension () const throw (CharacteristicTooLargeException, NotSupportedException)
	Build a primitive extension of degree p as in [DFS '09, Section 3].
const Field< T > &	ArtinSchreierExtension (const FieldElement< T > &alpha) const throw (CharacteristicTooLargeException, NotIrreducibleException, NotSupportedException, IllegalCoercionException)
	Build the splitting field of the polynomial 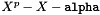$X^p - X - \mathtt{alpha}$ as in [DFS '09, Section 6].
FieldElement< T >	Couveignes2000 (const FieldElement< T > &alpha) const throw (IllegalCoercionException, IsIrreducibleException)
	Finds a root of the polynomial 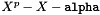$X^p - X - \mathtt{alpha}$ .
Properties
BigInt	characteristic () const throw ()
	The characteristic of the field.
long	degree () const throw ()
	The degree over the prime field F_p.
ZZ	cardinality () const throw ()
	The cardinality of the field.
long	ArtinSchreierHeight () const throw ()
	The constructed Artin-Schreier height.
FieldPolynomial< T >	generatingPolynomial () const throw ()
	The polynomial with coefficients in subField() that has been used to generate this extension.
FieldPolynomial< T >	primitivePolynomial () const throw ()
	The polynomial with coefficients in F_p used to represent elements of this field.
Field Elements
Routines to create elements of the field.
FieldElement< T >	scalar (const BigInt &i) const throw ()
	The element i mod p.
FieldElement< T >	zero () const throw ()
	The zero element of this field.
FieldElement< T >	one () const throw ()
	The identity element of this field.
FieldElement< T >	generator () const throw ()
	The generator over subField().
FieldElement< T >	primitiveElement () const throw ()
	The generator over F_p
FieldElement< T >	random () const throw ()
	A random element of the field.
Access to the Infrastructure
These methods let you use the internal `NTL` representation of elements to build a FieldElement or a FieldPolynomial. Warning These methods are for advanced use only. Use them if you want to use an algorithm by you or in NTL that is not available for FieldElement or FieldPolynomial.
void	switchContext () const throw ()
	Set the current context to this field's context.
FieldElement< T >	fromInfrastructure (const GFp &e) const throw ()
	Build an element of this field from an `NTL` type.
FieldElement< T >	fromInfrastructure (const GFpE &e) const throw (IllegalCoercionException)
	Build an element of this field from an `NTL` type.
FieldPolynomial< T >	fromInfrastructure (const GFpX &P) const throw ()
	Build an polynomial with coefficients in this field from an `NTL` type.
FieldPolynomial< T >	fromInfrastructure (const GFpEX &P) const throw (IllegalCoercionException)
	Build an polynomial with coefficients in this field from an `NTL` type.
Field lattice navigation
These routines permit to move around in the lattice of fields created by calls to ArtinSchreierExtension() as described in section Lattices of fields.
const Field< T > &	primeField () const throw ()
	The prime field F_p of this field.
const Field< T > &	baseField () const throw ()
	The base field of the Artin-Schreier tower.
const Field< T > &	subField () const throw (NoSubFieldException)
	The immediate subfield in the primitive tower.
const Field< T > &	overField () const throw (NoOverFieldException)
	The immediate overfield in the primitive tower.
const Field< T > &	stemField () const throw ()
	The field on the primitive tower isomorphic to this field.
Applying the isomorphism
These routines implement the algorithms of [DFS '09, Section 6.2] that convert elements written on the univariate basis of the primitive Artin-Schreier tower to and from the multivariate basis of any isomorphic tower.
void	toBivariate (const FieldElement< T > &e, vector< FieldElement< T > > &v) const throw (IllegalCoercionException)
	Convert the univariate representation of e to the multivariate representation over this field.
void	toUnivariate (const vector< FieldElement< T > > &v, FieldElement< T > &e) const throw (NotInSameFieldException, IllegalCoercionException)
	Convert the multivariate representation of v to the univariate representation of this field.
Predicates
bool	operator== (const Field< T > &F) const throw ()
	Equality.
bool	operator!= (const Field< T > &F) const throw ()
	Inequality.
bool	isIsomorphic (const Field< T > &F) const throw ()
	This field is isomorphic to F.
bool	isSubFieldOf (const Field< T > &F) const throw ()
	This field is contained in F.
bool	isOverFieldOf (const Field< T > &F) const throw ()
	This field contains F.
bool	isPrimeField () const throw ()
	This is a prime field.
bool	isBaseField () const throw ()
Printing
ostream &	print (ostream &o) const
	Print details about the field to o.

Static Public Member Functions
Instantiators
All instantiators are static. There's no constructor for Field objects.
static const Field< T > &	createField (const bool test=true) throw (NotPrimeException, NotIrreducibleException)
	Default instantiator, builds a field from `NTL`'s context.
static const Field< T > &	createField (const GFpX &P, const bool test=true) throw (NotPrimeException, NotIrreducibleException)
	Build a field from an irreducible polynomial P.
static const Field< T > &	createField (const BigInt &p, const long d=1, const bool test=true) throw (NotPrimeException, BadParametersException)
	Build the field F_p^d using a default polynomial.

Data Fields
Public data members
const BigInt	p
	The characteristic of the field.
const long	d
	The degree over the prime field F_p.
const long	height
	The constructed Artin-Schreier height.

Related Functions
(Note that these are not member functions.)
template<class T >
ostream &	operator<< (ostream &o, const Field< T > &F)
	Print details about F to o.

Local types
Local types defined in this class. They are aliases to simplify the access to the Infrastructure T and its subtypes. See Also Infrastructures
typedef T	Infrastructure
	A link to the Infrastructures Infrastructure.
typedef T::GFp	GFp
typedef T::MatGFp	MatGFp
typedef T::VecGFp	VecGFp
typedef T::GFpX	GFpX
typedef T::GFpE	GFpE
typedef T::GFpEX	GFpEX
typedef T::BigInt	BigInt
typedef T::Context	Context
typedef T::GFpXModulus	GFpXModulus

Detailed Description

template<class T>
class FAAST::Field< T >

A finite field.

Objects of this class can only be built through the static instantiators createField() and can never be destroyed.

The way the arithmetics of the field are actually implemented is given by the template parameter T that must be one of the Infrastructures. Note that changing the Infrastructure may sensibly change the speed of your code.

Template Parameters

T	An Infrastructure. It specfies which `NTL` types will carry out the arithmetic operations.

Todo:: Field objects are immortal. A better memory management involving garbage collection may be implemented one day.

Examples:: test.c++, testIso.c++, testLE.c++, testStem.c++, testTraceFrob.c++, and using_infrastructure.c++.

Member Function Documentation

template<class T >

const Field< T > & FAAST::Field< T >::ArtinSchreierExtension ( ) const throw (CharacteristicTooLargeException, NotSupportedException)

Build a primitive extension of degree p as in [DFS '09, Section 3].

Returns: A reference to the newly created Field object.

Exceptions

CharacteristicTooLargeException	If p is a multiprecision integer larger than the largest single precision integer.
NotSupportedException	If d is divisible by p and the generator of this field has trace 0. See creteField() and [DFS '09] for necessary and sufficient conditions for this not to hold.

Examples:: test.c++, testIso.c++, testLE.c++, testStem.c++, and testTraceFrob.c++.

template<class T >

const Field< T > & FAAST::Field< T >::ArtinSchreierExtension ( const FieldElement< T > & alpha ) const throw (CharacteristicTooLargeException, NotIrreducibleException, NotSupportedException, IllegalCoercionException)

Build the splitting field of the polynomial 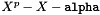$X^p - X - \mathtt{alpha}$ as in [DFS '09, Section 6].

The polynomial must be reducible (equivalently alpha must have trace 0). A primitive Artin-Schreier extension is constructed using ArtinSchreierExtension(), then Couveignes2000() is used in such an extension to find one of the roots and the isomorphic field is constructed. The computed root is used in pushDown() and liftUp() to navigate the tower as in [DFS '09, Section 6.2].

Returns: A reference to the newly created Field object.

See Also: ArtinSchreierExtension(), Couveignes2000(), pushDown(), liftUp().

Exceptions

CharacteristicTooLargeException	If p is a multiprecision integer larger than the largest single precision integer.
NotIrreducibleException	If alpha has trace 0.
NotSupportedException	If the primitive field cannot be created. See ArtinSchreierExtension() for details
IllegalCoercionException	If alpha cannot be coerced to an element of this field.

template<class T>

long FAAST::Field< T >::ArtinSchreierHeight ( ) const throw ()

inline

The constructed Artin-Schreier height.

Returns: The same value as height.

template<class T >

const Field< T > & FAAST::Field< T >::baseField ( ) const throw ()

The base field of the Artin-Schreier tower.

The Artin-Schreier height 0 subfield of this field.

Returns: A reference to the base field.

See Also: ArtinSchreierExtension(), height, ArtinSchreierHeight(), Lattices of fields.

Examples:: test.c++.

template<class T>

BigInt FAAST::Field< T >::characteristic ( ) const throw ()

inline

The characteristic of the field.

Returns: The same value as p.

template<class T >

FieldElement< T > FAAST::Field< T >::Couveignes2000 ( const FieldElement< T > & alpha ) const throw (IllegalCoercionException, IsIrreducibleException)

Finds a root of the polynomial 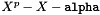$X^p - X - \mathtt{alpha}$ .

It uses the algorithm described in [Couveignes '00] and [DFS '09, Section 6.1].

Exceptions

IllegalCoercionException	if alpha cannot be coerced to this field.
IsIrreducibleException	If the polynomial is irreducible (equivalently, if alpha has trace 0).

template<class T >

const Field< T > & FAAST::Field< T >::createField ( const bool test = true ) throw (NotPrimeException, NotIrreducibleException)

static

Default instantiator, builds a field from NTL's context.

Parameters

[in] test If false, do not perform primality and irreducibility tests.

Returns: A reference to the newly created Field object.

Exceptions

NotPrimeException	If the current `NTL` modulus, as obtained by T::GFp::modulus(); is not a prime (unless T is GF2_Algebra).
NotIrreducibleException	If the current `NTL` modulus, as obtained by T::GFpE::modulus(); is not an irreducible polynomial.

Warning: If the current modulus has degree d divisible by the characteristic and if its (d - 1)-th coefficient is 0, then you won't be able to construct Artin-Schreier extensions through a call to ArtinSchreierExtension(). In fact in this case the generator of the field has trace 0 and the costruction of [DFS '09] doesn't work.

Examples:: test.c++, testIso.c++, testLE.c++, testStem.c++, testTraceFrob.c++, and using_infrastructure.c++.

template<class T >

const Field< T > & FAAST::Field< T >::createField	(	const GFpX &	P,
		const bool	test = `true`
	)		throw (NotPrimeException, NotIrreducibleException)

static

Build a field from an irreducible polynomial P.

Build the field F[X]/P(X).

T::GFp::modulus

must be set accordingly, unless T is GF2_Algebra.

Parameters

[in]	P	An irreducible polynomial.
[in]	test	If false, do not perform primality and irreducibility tests.

Returns: A reference to the newly created Field object.

Exceptions

NotPrimeException	If the current `NTL` modulus, as obtained by T::GFp::modulus(); is not a prime (unless T is GF2_Algebra).
NotIrreducibleException	If P is not an irreducible polynomial.

Warning: If P has degree d divisible by the characteristic and if its (d - 1)-th coefficient is 0, then you won't be able to construct Artin-Schreier extensions through a call to ArtinSchreierExtension(). In fact in this case the generator of the field has trace 0 and the costruction of [DFS '09] doesn't work.

template<class T >

const Field< T > & FAAST::Field< T >::createField	(	const BigInt &	p,
		const long	d = `1`,
		const bool	test = `true`
	)		throw (NotPrimeException, BadParametersException)

static

Build the field F_p^d using a default polynomial.

Notice that this operation implicitely creates the field F_p too.

Parameters

[in]	p	A prime number.
[in]	d	A positive integer.
[in]	test	If false, do not perform a primality test on p.

Returns: A reference to the newly created Field object.

Exceptions

NotPrimeException	If p is not prime
BadParametersException	If d is less than one.
BadParametersException	If T is GF2_Algebra and p is different from 2.

Todo:: For the moment the default polynomial is generated randomly. When p divides d , this prevents from building successive Artin-Schreier extensions if the (d - 1)-th coeffcient of the randomly generated polynomial is 0. In fact in this case the generator of the field has trace 0 and the costruction of [DFS '09] doesn't work. It would be nice to have a better generation routine that discards such polynomials.

template<class T>

long FAAST::Field< T >::degree ( ) const throw ()

inline

The degree over the prime field F_p.

Returns: The same value as d.

template<class T >

FieldElement< T > FAAST::Field< T >::fromInfrastructure ( const GFp & e ) const throw ()

Build an element of this field from an NTL type.

Returns a new element of this field having e as representation.

Parameters

[in] e An NTL scalar element.

Returns: The newly created element.

Warning: e must have been created in the context of this field. See switchContext().

See Also: using_infrastructure.c++

template<class T >

FieldElement< T > FAAST::Field< T >::fromInfrastructure ( const GFpE & e ) const throw (IllegalCoercionException)

Build an element of this field from an NTL type.

Returns a new element of this field having e as representation.

Parameters

[in] e an NTL element.

Returns: The newly created element.

Exceptions

IllegalCoercionException If this field is a prime field only scalar elements can belong to it. Use fromInfrastructure(const GFp&) const instead.

Warning: e must have been created in the context of this field. See switchContext().

See Also: using_infrastructure.c++

template<class T >

FieldPolynomial< T > FAAST::Field< T >::fromInfrastructure ( const GFpX & P ) const throw ()

Build an polynomial with coefficients in this field from an NTL type.

Returns a new polynomial over this field having P as representation.

Parameters

[in] P an NTL scalar polynomial.

Returns: The newly created element.

Warning: P must have been created in the context of this field. See switchContext().

See Also: using_infrastructure.c++

template<class T >

FieldPolynomial< T > FAAST::Field< T >::fromInfrastructure ( const GFpEX & P ) const throw (IllegalCoercionException)

Build an polynomial with coefficients in this field from an NTL type.

Returns a new polynomial over this field having P as representation.

Parameters

[in] P an NTL polynomial.

Returns: The newly created element.

Exceptions

IllegalCoercionException If this field is a prime field only scalar polynomials can belong to it. Use fromInfrastructure(const GFpX&) const instead.

Warning: P must have been created in the context of this field. See switchContext().

See Also: using_infrastructure.c++

template<class T >

FieldPolynomial< T > FAAST::Field< T >::generatingPolynomial ( ) const throw ()

The polynomial with coefficients in subField() that has been used to generate this extension.

Or X - 1 if this is a prime field.

See Also: [DFS '09].

Invariant: This is the minimal polynomial of generator().

template<class T>

FieldElement<T> FAAST::Field< T >::generator ( ) const throw ()

inline

The generator over subField().

Returns: A root of generatingPolynomial().

template<class T>

bool FAAST::Field< T >::isBaseField ( ) const throw ()

inline

This is the base field of an ArtinSchreier tower

template<class T>

bool FAAST::Field< T >::isIsomorphic ( const Field< T > & F ) const throw ()

inline

This field is isomorphic to F.

Returns: true only if the isomorphism has been computed.

See Also: stemField().

template<class T>

bool FAAST::Field< T >::isOverFieldOf ( const Field< T > & F ) const throw ()

inline

This field contains F.

Returns: true only if the inclusion has been computed.

See Also: overField()

template<class T >

bool FAAST::Field< T >::isSubFieldOf ( const Field< T > & F ) const throw ()

This field is contained in F.

Returns: true only if the inclusion has been computed.

See Also: subField().

template<class T>

bool FAAST::Field< T >::operator!= ( const Field< T > & F ) const throw ()

inline

Inequality.

Note: Comparison on the address of the object.

template<class T>

bool FAAST::Field< T >::operator== ( const Field< T > & F ) const throw ()

inline

Equality.

Note: Comparison on the address of the object.

template<class T>

const Field<T>& FAAST::Field< T >::overField ( ) const throw (NoOverFieldException)

inline

The immediate overfield in the primitive tower.

If this field belongs to the primitive tower (the stem), then its immediate overfield is returned. Otherwise stemField().overField() is returned.

Returns: A reference to the overfield.

Exceptions

NoOverFieldException If no overfield as been constructed through a call to ArtinSchreierExtension()

See Also: ArtinSchreierExtension(), Lattices of fields.

template<class T>

FieldElement<T> FAAST::Field< T >::primitiveElement ( ) const throw ()

inline

The generator over F_p

Returns: A root of primitivePolynomial().

Invariant: This is the same as generator() for primitive fields built using ArtinSchreierExtension().

template<class T >

FieldPolynomial< T > FAAST::Field< T >::primitivePolynomial ( ) const throw ()

The polynomial with coefficients in F_p used to represent elements of this field.

Or X - 1 if this is a prime field.

See Also: [DFS '09].

Invariant: This is the minimal polynomial of primitiveElement().

template<class T >

FieldElement< T > FAAST::Field< T >::scalar ( const BigInt & i ) const throw ()

The element i mod p.

Parameters

[in] i An integer.

Returns: An element of this field.

template<class T>

const Field<T>& FAAST::Field< T >::stemField ( ) const throw ()

inline

The field on the primitive tower isomorphic to this field.

If this field belongs to the primitive tower, then it returns itself. Otherwise it returns the field in the primitive tower (the stem) that is isomorphic to this field. The isomorphism has been computed through Couveignes2000(const FieldElement<T>&) const as described in ArtinSchreierExtension(const FieldElement<T>&) const.

Returns: A reference to the stem field.

See Also: ArtinSchreierExtension(), Couveignes2000, Lattices of fields

Examples:: testIso.c++.

template<class T>

const Field<T>& FAAST::Field< T >::subField ( ) const throw (NoSubFieldException)

inline

The immediate subfield in the primitive tower.

If this field belongs to the primitive tower (the stem), then its immediate subfield is returned. Otherwise stemField().subField() is returned.

Returns: A reference to the subfield.

Exceptions

NoSubFieldException If this is a prime field.

See Also: ArtinSchreierExtension(), Lattices of fields.

template<class T >

void FAAST::Field< T >::switchContext ( ) const throw ()

Set the current context to this field's context.

NTL's context holds information about the modulus and the characteristic of a finite field. By calling this method you set the current NTL context to this field's context, so that any subsequent operation on NTL types such as T::GFpX or T::GFpE will use that context.

You usually shouldn't be concerned about this method as the library takes care of switching the context for you when needed. The only time when you have to explicitly call it is when you want to use NTL types outside of the library and then transform the result to a FieldElement or FieldPolynomial through a call to a fromInfrastructure() method.

Warning: Be aware that the current context is undefined after any call to a function of this library.

See Also: using_infrastructure.c++

template<class T >

void FAAST::Field< T >::toBivariate	(	const FieldElement< T > &	e,
		vector< FieldElement< T > > &	v
	)		const throw (IllegalCoercionException)

Convert the univariate representation of e to the multivariate representation over this field.

If this is a prime field, then v is filled with the coefficients in F_p of its univariate representation. Otherwise let

x = e.parent().generator();

This method fills the vector v with p elements of this field such that

$\begin{equation} \mathtt{e} = \mathtt{v[0]} + \mathtt{v[1]}*\mathtt{x} + ... + \mathtt{v[p-1]}*\mathtt{x}^{p-1} \mathrm{.} \end{equation}$

Let K be this field, this corresponds to convert e from its internal (univariate) representation to the bivariate representation as an element of K[x]. A repeated application of this method implements ApplyInverse of [DFS '09, Section 6.2].

Parameters

[in]	e	An element of any field isomorphic to overField().
[out]	v	A vector of elements of this field that satisfies condition (1).

Exceptions

IllegalCoercionException If the field e belongs to is not isomorphic to overField().

Invariant: When e belongs to a field in the primitive tower (the stem), this is equivalent to pushDown(e, v) and then coerce all the contents of v to this field.

See Also: pushDown().

Examples:: testIso.c++.

template<class T >

void FAAST::Field< T >::toUnivariate	(	const vector< FieldElement< T > > &	v,
		FieldElement< T > &	e
	)		const throw (NotInSameFieldException, IllegalCoercionException)

Convert the multivariate representation of v to the univariate representation of this field.

If the elements of v belong to the prime field, then e is the element whose univariate representation has v as cofficients. Otherwise let

x = generator();

This method stores in e an element of this field such that

$\begin{equation} \mathtt{e} = \mathtt{v[0]} + \mathtt{v[1]}*\mathtt{x} + ... + \mathtt{v[p-1]}*\mathtt{x}^{p-1} \mathrm{,} \end{equation}$

If v is too short, it is filled with zeros. If v is too long, the unnecessary elements are ignored.

Let K be the field containing the elements of v, this corresponds to convert v from the multivariate representation as an element of K[x] to the internal (univariate) representation of this field. A repeated application of this method implements ApplyIsomorphism of [DFS '09, Section 6.2].

Parameters

[in]	v	A vector of elements all belonging to a field isomorphic to subField().
[out]	e	An element of this field satisfying condition (2).

Exceptions

NotInSameFieldException	If the elements of v do not belong all to the same field.
IllegalCoercionException	If the field the elements of v belong to is not isomorphic to subField().

Invariant: When this field is in the primitive tower (the stem), this is equivalent to coerce all the contents of v to the stem and then liftUp(v, e) .

See Also: liftUp().

Examples:: testIso.c++.

Field Documentation

template<class T>

const long FAAST::Field< T >::height

The constructed Artin-Schreier height.

This is the number of intermediate Artin-Schreier extensions over baseField() that have been constructed using the the techniques of [DFS '09, Sections 3 and 6].

Invariant: The following formula is always true: $[\mathtt{K} : \mathtt{K.baseField()}] = p^\mathtt{height}$

Public Member Functions

Static Public Member Functions

Data Fields

Related Functions

Local types

Detailed Description

template<class T> class FAAST::Field< T >

Member Function Documentation

Field Documentation

template<class T>
class FAAST::Field< T >