FAAST offers an intuitive object-oriented interface to handle finite fields and their extensions. The three main types you will use are Field, FieldElement and FieldPolynomial, which are described in the section Finite Field Arithmetics.

FAAST adds some genericity on top of the traditional NTL architecture, one of its most prominent features is the mechanism of Infrastructures which uses C++ templates to let you choose statically (at compile-time) which set of NTL algorithms use.

All in all, the goal of FAAST is to represent Lattices of fields and give algorithms to work into them. For the moment FAAST is limited to some special types of lattices arising from Artin-Schreier towers. See Lattices of fields for more details.

Finite Field Arithmetics

This module contains three types, namely FAAST::Field, FAAST::FieldElement and FAAST::FieldPolynomial, which represent, respectively, finite fields, elements of finite fields and polynomials with coefficient over finite fields.With some notable exception (see FieldElement() and FieldPolynomial()), each FAAST::FieldElement and FAAST::FieldPolynomial belongs to a FAAST::Field object called its parent field. Elements (and polynomials) having the same parent field can be combined (added, multiplied, etc.) freely, while limitations apply for combining elements belonging to two different fields; see FAAST::FieldElement and FAAST::FieldPolynomial.Elements (and polynomials) can be moved from one field to another when a morphism is known; see Lattices of fields.

See the module Finite Field Arithmetics for the list of methods and functions.

Infrastructures

NTL provides three different ways of representing modular integers:

zz_p is a class representing modular integers with word-sized modulus,
ZZ_p is a class representing modular integers with arbitrary sized modulus,
GF2 is a class representing integers modulo 2.

To each of these types corresponds a whole family of types (ZZ_p_X, GF2_E, etc.) representing polynomials with modular coefficients, modular polynomials with modular coefficients, etc. The actual algorithms implementing arithmetics for such types vary and affect remarkably the performances of FAAST. See the NTL manual for more details.Infrastructures are collections (struct 's) of types providing genericity over NTL types. They provide an unique set of names to abstract from the implementation details of the three NTL families ZZ_p*, zz_p* and GF2*. You must provide an Infrastructure as template parameter to the types and most of the functions of FAAST. This parameter tells FAAST which of the three NTL families it should use to perform modular arithmetics.Here's an example of how to use the infrastructure FAAST::zz_p_Algebra. First some typedef 's to save typing:

typedef Field<zz_p_Algebra>  gfp;
typedef FieldElement<zz_p_Algebra>  gfp_E;
typedef FieldPolynomial<zz_p_Algebra>  gfp_X;

Then define some parameters (characteristic, degree, etc.), notice the use of FAAST::Field::Infrastructure as an alias for FAAST::zz_p_Algebra (useful if you later change your mind about the Infrastructure):

gfp::Infrastructure::BigInt p;

long d, l;

Finally create a finite field:

const gfp* K = &(gfp::createField(p,d));

If you are wondering which Infrastructure you should use, then use FAAST::zz_p_Algebra, as it is quite flexible and way faster than FAAST::ZZ_p_Algebra.If you plan to construct fields with huge characteristics (larger than the largest long), then you should opt for FAAST::ZZ_p_Algebra; notice however that FAAST does not let you build Artin-Schreier extensions in characteristics greater than the greatest long, so you will probably miss its most exciting features.Finally, if you only work in characteristic 2 and care about performance, you should consider compiling NTL with the gf2x library and using FAAST::GF2_Algebra as Infrastructure. If you don't use the gf2x library, then FAAST::GF2_Algebra will only be interesting for moderate field cardinalities, but it will give the pace up to FAAST::zz_p_Algebra for huge fields.

See the module Infrastructures for more details.

Lattices of fields

The most exciting feature of FAAST is its ability to deal with field extension and keep track of morphisms. This ability is limited to Artin-Schreier towers as described in [DFS '09] and [Couveignes '00] and gives rise to lattices of a special form; we call them stem lattices.

For the rest of this section p will be the characteristic of our fields. Remind that an Artin-Schreier extension is a field extension of degree p generated by an irreducible polynomial of the form

$X^p - X - a\mathrm{.}$

The simplest lattice is the lattice formed by a single field. Finite fields of arbitrary cardinality can be built through the static instantiators Field::createField(). Suppose you build the field with p elements F_p then the resulting lattice looks like

$F_p$

When you build non-prime fields, the prime subfield is automatically constructed. Suppose you build a field named K₀, then the resulting lattice looks like

$\xymatrix{ \mathbf{K}_0 \ar@{-}[d]\\ F_p }$

Now, to add fields to a lattice there is two methods, namely Field::ArtinSchreierExtension() const and Field::ArtinSchreierExtension(const FieldElement&) const. Both create an Artin-Schreier extension, but they differ in the way the extension is created. The former method chooses a default irreducible Artin-Schreier polynomial such that the generated Artin-Schreier extension is primitive in the sense of [DFS '09, Section 3]. The resulting lattice is then

$\xymatrix{ \mathbf{K}_1\ar@{-}[d]^p\\ \mathbf{K}_0 \ar@{-}[d]\\ F_p }$

The latter method constructs the splitting fields of the polynomial 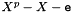$X^p - X - \mathtt{e}$ where e is the FieldElement given as a parameter. Assuming that the polynomial is irreducible, it constructs a primitive extension using Field::ArtinSchreierExtension() const and then uses the isomorphism algorithm of [Couveignes '00] to establish an isomorphism between the primitive field and the splitting field. So for example a call to

K0.ArtinSchreierExtension(e);

would generate a lattice

$\xymatrix{ \mathbf{K}_1\ar@{-}[d]^p & \mathbf{L}_1\ar@{~}[l]\\ \mathbf{K}_0 \ar@{-}[d]\\ F_p }$

where K₁ is the primitive extension and U₁ is the field generated by 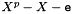$X^p - X - \mathtt{e}$ .

All the objects of type Field are persistent: once they are created they are never destroyed. So, even if you don't hold a reference to K₁, another call to

K0.ArtinSchreierExtension(e2);

will not create a new primitive field, it will use K₁ instead. The resulting lattice would be

$\xymatrix{ \mathbf{M}_1\ar@{~}[r] & \mathbf{K}_1\ar@{-}[d]^p & \mathbf{L}_1\ar@{~}[l]\\ & \mathbf{K}_0 \ar@{-}[d]\\ & F_p }$

By repeatedly mixing calls to the two methods, one ends up with lattices of the form

$\xymatrix{ \mathbf{W}_n\ar@{~}[r] & \mathbf{K}_n\ar@{--}[dd] & \mathbf{Z}_n\ar@{~}[l]\\ \\ \mathbf{U}_2\ar@{~}[r] & \mathbf{K}_2\ar@{-}[d]^p & \mathbf{V}_2\ar@{~}[l]\\ \mathbf{M}_1\ar@{~}[r] & \mathbf{K}_1\ar@{-}[d]^p & \mathbf{L}_1\ar@{~}[l]\\ & \mathbf{K}_0 \ar@{-}[d]\\ & F_p }$

Now the reason why we call this a stem lattice should be clear. In the middle there's the primitive tower (K₀, K₁, ..., K_n), in the sense of [DFS '09, Section 3], which we call the stem. The stem is organized in levels, each level being an extension of degree p over the lower one (with the only possible exception of the extension K₀/F_p). At each level, a set of fields all isomorphic to that level forms the spurs.

The methods Field::subField(), Field::overField(), Field::baseField(), Field::primeField() and Field::stemField() let you navigate field lattices.

Coercion operators (see FieldElement and FieldPolynomial) let you move elements from one field to the other, provided that the element belongs to both fields. So for example you can move elements from K₀ or M₁ to L₁, but it will not always be possible to move an element from K₂ to K₁. For example, coercion from K₀ to K₁ is as easy as

e0 = K0.random();

e1 = e0 >> K1;

In case a coercion is not possible, an IllegalCoercionException is issued.

Another way of moving around in field lattices is to use the vector space morphisms between the levels of the lattice. The functions pushDown() and liftUp() let you express the morphism between two adjacent levels of the stem, while Field::toBivariate() and Field::toUnivariate() let you express the morphisms between to arbitrary spurs in two adjacent levels. Notice that there is no need to know what the order of the calls to Field::ArtinSchreierExtension() was in order to apply these methods: any field of a level can be considered as an Artin-Schreier extension over any other field in the lower level.

Exceptions

See the Exceptions module for a list of all the exceptions thrown by methods and functions of this library.